移動現象論とは？　身近な例を紹介

資料請求番号：TS52

はじめに（移動現象論で何がわかるの？）

まず、移動現象論を学べばどんなことが出来るようになるのかと言いますと・・・

• 水槽に垂らしたインクの濃度が均一になるのにかかる時間はどれくらい？
• コップに入れたお湯が冷めるのに必要な時間はどれくらい？
• 味噌汁をお椀に入れた時に出るモヤモヤはなぜできるの？
• 魔法瓶はなぜ保温、保冷ができるの？
• サラサラな液体と粘っこい液体をストローで吸い出すときに必要な力の差は？

といった疑問を解決することができるようになります。
こうして見てみると、「移動現象論」という学問分野に馴染みのない人は多いと思いますが、ほとんどの人が移動現象というのを普段から目の当たりにしていると思います。
それでは始めましょう。

移動現象論とは一言でいうと

「物質量、運動量、熱量といった物理量が移動する速さについて取り扱う学問」

物理量の移動とは？

物質量を例にとってみたいと思います。例えば、水槽の中にインクを垂らしたとします。
そしたらインクはどうなりますか？何もしなくてもインクはどんどん広がっていきますよね。終いには水槽の中全体がインクの色に染まってしまいます。
この現象についてよく考えてみてください。水槽は完全に静置した状態、別にかき混ぜてもいない、それなのにインクは勝手に（自発的に）広がっていきます。
インクが勝手に広がっていく。これは「物質量は多いところから少ないところ移動する」という自然の法則に則った現象なのです。

水槽にインクを垂らした直後は、垂らした部分だけインクの成分が集まっていて、それ以外の部分はインクの成分がほとんどない状態です。この状態に自然の法則を当てはめると、インクの成分の濃いところから薄いところへインクの成分が移動していきます。しばらく放置すると、水槽の中全体がインクの色に染まります。

移動の速さを表す式

「物質量は多いところから少ないところに移動する」という原則から「移動の速さ」について考えてみましょう。
物質量の移動の速さを表す式は次の通りです。

Jというのは単位時間、単位面積あたりに物質が移動する量です。単位を示すなら[mol･m^-2･s^-1]です。単位面積当たりという要素が入っていますが、[mol･s^-1]から移動の速さを表していることに納得いただけましたでしょうか？

次に右辺を見てみましょう。Dというのは拡散係数[m²･s^-1]です。これは定数で、物質に固有です。インクを例にとれば広がりやすいインクなのかどうなのか？という指標ですね。そして大事なのが

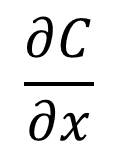
です。Cが濃度(単位体積あたりの物質量)[mol･m^-3]、xが位置[m]を表します。そして∂は偏微分記号ですが微分は傾きを表すという原則を思い出せば、上の式は「濃度勾配」を表わしているということが分かります。

まとめると、物質量の移動の速さというのは
定数×濃度勾配
で表現できるのです。ものすごい濃いところとものすごい薄いところが接すると、速く物質が移動するということを表しています。

移動現象のアナロジー

アナロジーとは「類似性」を意味します。これまで物質量の移動を例にインクの話を進めてきました。
インクの移動速度は定数×濃度勾配でしたね。
熱量、運動量でも「類似した扱い」をすることが出来るのです。
例えば熱量の場合は「熱量は多いところから少ないところに移動する」
運動量の場合は「運動量は多いところから少ないところに移動する」といったように。

「熱量が多い」というのはすなわち「熱い」ということを意味します。熱いものと冷たいものを接触して置いておくと終いには温度が一緒になりますよね。
これは「熱いものから冷たいものへ熱量が移動した」ということになります。
その速度は

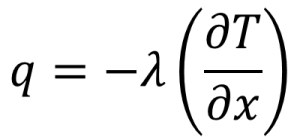
です。Jというのは単位時間、単位面積あたりに熱量が移動する量です。単位を示すなら[J･m^-2･s^-1]です。熱量の移動の速さを表しているのです。
λは熱伝導率(定数)、Tは温度、xは位置です。

は温度勾配を表しています。つまり、熱量の移動速度は
定数×温度勾配
で表現できます。

物質量の移動速度を表す「定数×濃度勾配」に非常に似ていますよね。

運動量の移動の式も

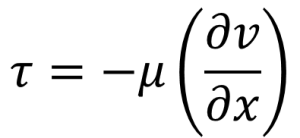
定数×速度勾配なのです。

まとめ

移動現象論というのは「物質量、運動量、熱量といった物理量が移動する速さについて取り扱う学問」です。インクの広がる速度は？コップの中のお湯が冷める速度は？といった疑問に答える学問です。
物理量(物質量、熱量、運動量)は

• 多いところから少ないところに移動する
• その速度は勾配に比例する

という原則に従っています。
いかがでしょうか？少しでも移動現象論を身近
に感じていただければ幸いです。