資料請求番号:TS32
CONTENTS
発散の数式と現象のイメージを結ぶ
流体力学、電磁力学には「∇・」といったベクトル解析の演算子がたくさん出てきます。このとき、ベクトル解析の内容をしっかり理解していないと、もうその時点でその分野の勉強が進まなくなってしまいます。ここでは、ベクトル解析の「発散」と呼ばれる演算子をテーマに、連続の式の導出を通して発散の定義(数式)と実際の現象のイメージを結び付けていただくことを目的とします。
発散の定義
ベクトル解析の基本を説明したページ(こちら)で発散について
「発散」の定義は以下の通りです。
あるベクトルuがあるとき、
その発散∇・uは
である。
と説明しました。このページでは発散の演算子が登場する「連続の式」の導出を行ったあと、発散の物理的イメージについて説明したいと思います。
連続の式
流体を小さい要素に分割して考える
連続の式は流体力学における基本の式で「流体が突然発生したり、消滅したりしない」ということをコンセプトとしています。流体が発生したり、消滅したりしないのを示すには、流体を非常に非常に小さい要素に分割して、その要素内に出入りする流体の量に過不足がないという方程式を立てればよいのです。
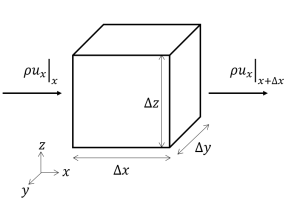
要素での流体の出入りを数式にする
上の要素に対して
(要素に蓄積する流体の量)= (要素に流入する流体の量)ー(要素から流出する流体の量)
という方程式を立てます。例えばこんな感じ
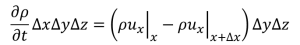 (1-1)
(1-1)
この方程式はお風呂にお湯がたまることをイメージしてください。蛇口をいっぱいひねればお湯の湯面が上がるスピードは速くなり、排水溝の穴を大きくすればお湯の湯面が下がるスピードは遅くなります。
(1-1)式の説明をします。ρは流体の密度[kg/m3]なので、ρΔxΔyΔz[kg]は流体の質量です。これの時間変化を取って、要素に蓄積する流体の量[kg/s]を表しています。
次に右辺を見てみます。uxに縦棒があってxと書いてありますが、位置xにおける流体のx方向の流速[m/s]を表しています。これにρをかけることで単位面積あたり、単位時間あたりに要素に流入する流体の量[kg・m-2・s-1]を表すことになります。流体の通る面の断面積はΔyΔz[m2]ですからρuxΔyΔzで単位時間あたりに要素に流入する流体の量[kg/s]になります。逆に要素から流出する流体の量は位置x+ΔxにおけるρuxΔyΔzになります。
※実際にはx面(面積ΔyΔz)へはx方向の流速だけでなく、y方向やz方向の流速があるのですが、検査体積を微小に取ればx面に対する流れは一様であり、「x方向のみ」と仮定することができます。
検査体積に流入する面はx面だけではなく、y面、z面もあります。そしてそれぞれの面に対応する方向の流速で流体が出入りします。
検査体積に流入、流出する流体の量をすべて書き出すと以下の式になります。
![]() (1-2)
(1-2)
式変形のコツ(テイラー展開)
ここで、テイラー展開の考え方を使って、x+Δx、y+Δy、z+Δzにおける物理量をx,y,zで表現します。例えば、こんな感じ。
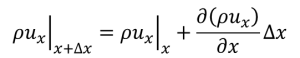 (1-3)
(1-3)
この式変形をy面、z面にも適用し、まとめると(1-2)式は(1-4)式になります。
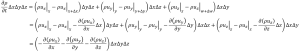 (1-4)
(1-4)
ちょっとばかし複雑に見えますが、同じことを3回やってるだけです。
(1-4)式をさらに整理して
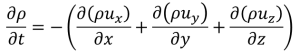 (1-5)
(1-5)
連続の式は「発散」で表現できる
(1-5)式を発散の定義に当てはめれば
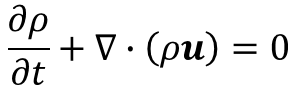 (1-6)
(1-6)
となります。特に非圧縮性流体(液体)では密度の変化は起こりませんので
![]() (1-7)
(1-7)
に簡略化されます。
発散の物理的イメージ
発散というのは「湧き出し」とも呼ばれます。連続の式は「流体が突然発生したり、消滅したりしない」ということをコンセプトとして、要素内に出入りする流体の量を調査して立てた式です。この結果が(1-7)式なのです。
また、(1-7)式の左辺が単位体積当たりの流れの増減を表していて、右辺で「それはないよ」と言っているという解釈の仕方もできると思います。
点電荷と電場について
非圧縮性流体ではどこからともなく何かが湧き出したり、吸い込まれたりすることはないのですが、それが当てはまらない例があります。それが電場です。
マクスウェル方程式の一つにこんなものがあります。
![]() (2-1)
(2-1)
点電荷ρがあると、ベクトルである電場Dが湧いて出てくるよということを表した式です。図にするとこんな感じです。

発散とは何なのか? まとめ
要素内に出入りする物の量を調査して現れた「発散」という概念は、ある単位体積で物理量が湧いて出てくるのか、吸い込まれるのか、それとも変わらないのかを教えてくれます。逆に「変わらない」ということを前提とすることで(1-7)式とナビエ・ストークス方程式を連立して流体の振る舞いを解くことができます。
 らい・ぶらり
らい・ぶらり
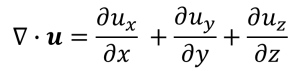


コメントを残す