資料請求番号:TS32
勾配の数式のわかりやすさを追求する
流体力学、電磁力学には「∇」といったベクトル解析の演算子がたくさん出てきます。このとき、ベクトル解析の内容をしっかり理解していないと、もうその時点でその分野の勉強が進まなくなってしまいます。ここでは、ベクトル解析の「勾配」と呼ばれる演算子をテーマに、勾配の定義(数式)と実際の現象のイメージを結び付け、頭の中をスッキリさせた状態にしていただくことが目的です。
はじめに
ベクトル解析の基本を説明したページ(こちら)で勾配について
「勾配」の定義は以下の通りです。
あるスカラー変数Tがあったとき、その勾配は
で表される。
と説明しました。このページではこの定義の物理的イメージについて書いてみたいと思います。
勾配のイメージ
偏微分
まず、偏微分について説明します。とある平面T(x,y)があるとします。Tは二変数関数でスカラーです。ここで、xとyの値を決めてあげればTの値が決まりますよね。ここで任意の点Aをとり、平面に沿ってΔxだけずらした点を点Bとおきます。ここで重要なポイントはy方向には一切ずらしません。これにより、Tは疑似的にxだけの関数と見なすことができます。
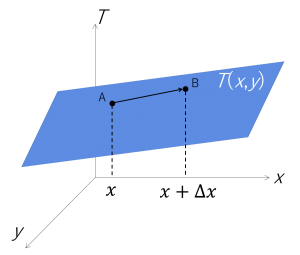
このとき、Δxをギューッと0に近づけていった時の値が「Tのx偏微分値 ∂T/∂x」です。微分の定義と同じで、ただ「y方向に変化しない」という仮定が加わっただけですね。

次に、任意の点Aから平面に沿ってΔyだけずらした点を点Cとします。今度はx方向に一切ずらしません。これでTを疑似的にyだけの関数と見なすことができます。
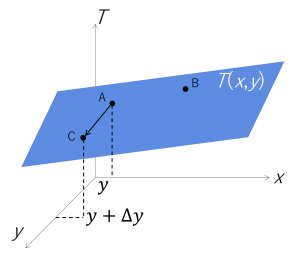

先ほどと同様にして「Tのy偏微分値 ∂T/∂y」も定義できました。
偏微分にベクトルの概念を入れてみる
点Aと点Bの間の傾きは∂T/∂xです。点Aと点Cの間の傾きは∂T/∂yです。では、点Aと点Dの間の傾きは??
ここでベクトルの概念が登場します。∂T/∂xにx方向を表す基底ベクトルiをつけて、∂T/∂yにy方向を表す基底ベクトルjをつけ、足し算してあげればAD間のベクトルが表現できます。

つまり

ということです。これはTの勾配そのものです。このように偏微分とベクトルを組み合わせて使うことにより、点Aから見た時の平面Tの傾きをどの方向でも表現できるようになりました。
ポテンシャル
勾配を使ってポテンシャルというものを表現することができます。力学的ポテンシャルUは力Fを使ってこんなふうに定義されます。
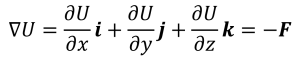
ポテンシャルというのは「潜在すること」という意味を持ちます。ポテンシャルUは坂道だと思ってください。坂道は勾配が大きいほど質点に大きな力を与えることができます。ポテンシャルUだけだとただの坂道ですが、そこに勾配という意味をつけることによって(∇をつけることによって)Fという力が生まれるのです。そしてその大きさは坂道の勾配に依存します。
以上が勾配とポテンシャルの説明です。厳密さを考えると少しいい加減な部分もあったかもしれませんが、厳密さよりも直感的なイメージを大切にしました。数式とイメージがリンクできるようになれば幸いです。
 らい・ぶらり
らい・ぶらり
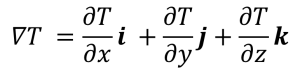


コメントを残す