資料請求番号：TS35

ポケモンのレートを統計学から分析

ポケモンのレートと実力の関係って？？

レート対戦をやったことのある方なら、少しは気になったことがあるかと思います。
そこで、今回はレートの数値と偏差値の関係を計算してみました。

ちなみに、私はポケモンエンジョイ勢でレートは1500台前半でございます。100戦くらいしてこのくらいなので、その程度の実力なんだな～と思います。

レートと偏差値の関係

統計学に基づいた考え方のもと、レートと偏差値の関係を計算してみると、以下のようになります。

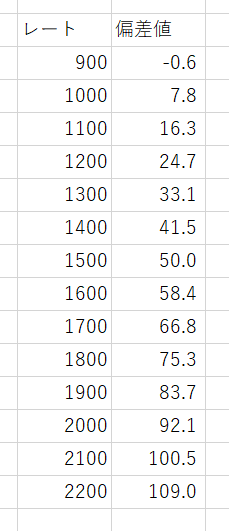
ポケモンのレートっていうのは、実は1500が偏差値50、すなわち平均なんだ。

へぇ～。1500ってあくまでスタートラインで、平均ってもっと高いもんだと思ってた～。

ネットの情報見てるとな、まるでレート1700くらいが普通のような見え方がするんだが、実は1500が平均、
というより、1500が平均になるように作られていると思うたい。

どうしてそんなこと言えるの？

統計学的手法で計算してみたら、平均がピッタリ1500になったんだ。標本数24万もあるのに、平均がぴったり1500になるなんて、気味悪いだろ？
だから俺はこのポケモンレートバトルは平均が1500になるように作られていると思ったったい。
多分だが、ポケモン作る側にその手の専門家がいるんだろうな。

レート1700って偏差値66.8なのね！ということは、大体上位４～５％ってこと？
スゴイじゃん！っていうか、スゴイじゃん！ワタシ！

オマエ、レート1700くらいあるのか？

うん！今、1724。

ふぅ～ん。まぁ、俺はエンジョイ勢なので興味ないが。

統計学的手法に基づいてレートの平均値、標準偏差、そして、レートと偏差値の関係を計算したところ、
1500が平均、1700は偏差値66.8であることがわかりました。偏差値66.8というのは上位約５％の人の数値です。

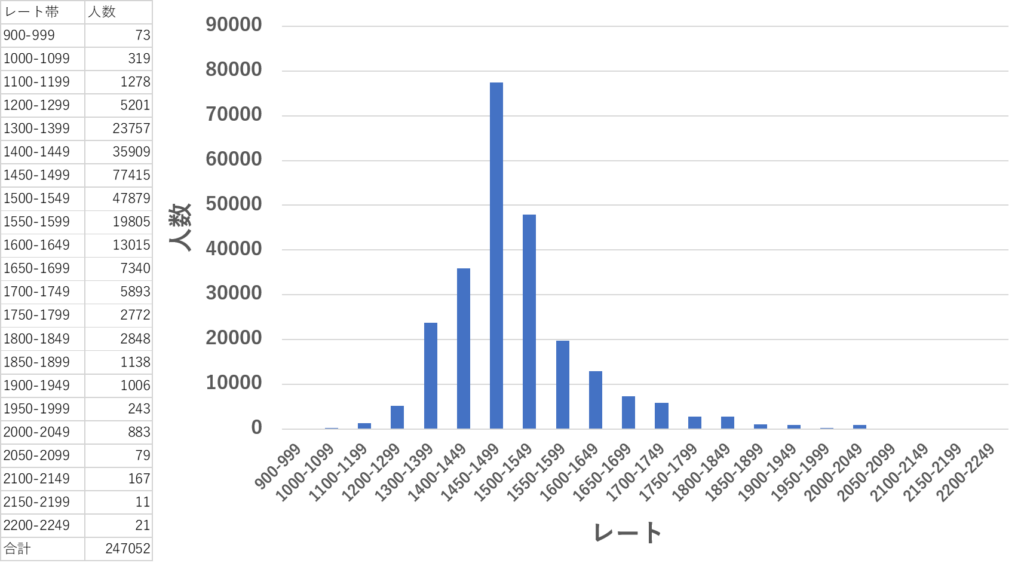
レートの平均・標準偏差の計算方法

これは、ヒストグラム（レート、得点、粒径などの分布）を元に計算したのかしら？

ああ。以前、ヒストグラムから平均・標準偏差、そして自分の偏差値を求める方法を解説しただろ？
あれと同じ方法で計算できるんだ。

 らい・ぶらり 

偏差値の計算方法～統計学から見た偏差値の考え方～

http://shimaphoto03.com/science/deviation/

資料請求番号：TS35偏差値は統計に基づいた指標であるメリークリスマスでございます。世の中の人々が現を抜かしている中、受験生は勉強に勤しんでいるかと思います。センター試験も近づいてきましたね。今回は、偏差値のお話をしたいと思います。偏差値。それは受験...

そして、以下のサイトにレート別人口というのが掲載されていたので、そのデータを引用させていただいた。

※今回の計算には以下のサイトのデータを使用させていただきました。
ポケモンスプレッドシート

これでヒストグラムが描けるのね！

そうだ。そして、以下の式を使って平均と標準偏差を求めることができる。

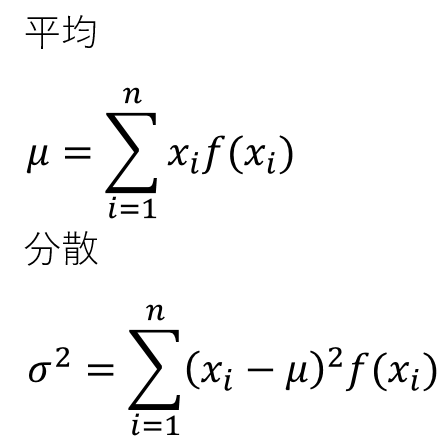
x_iはレート帯の中央値、例えば900～999だったら950と近似して・・・・
f(x_i)は確率密度関数。確率なんだから、全部足し合わせたときに１になるように、
レート帯別の人数を全体の人数で割るのよね。

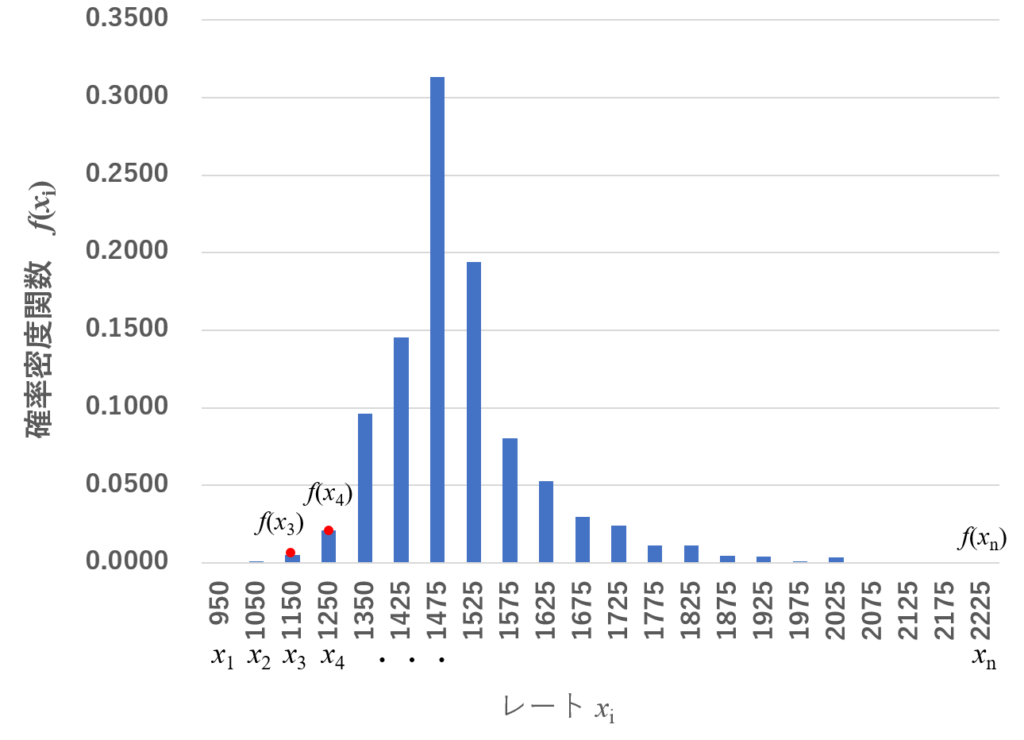
その通り。
・・・それにしても、レートバトルやっている人は24.7万人か～。すごい数だな。

昔も今も、他のゲーム、メディアとは一線を画しているよね。ポケモンは。24万人じゃあ、統計分析するには十分すぎる数だね。

上の式に基づいて、平均と標準偏差を求めてみたよ！

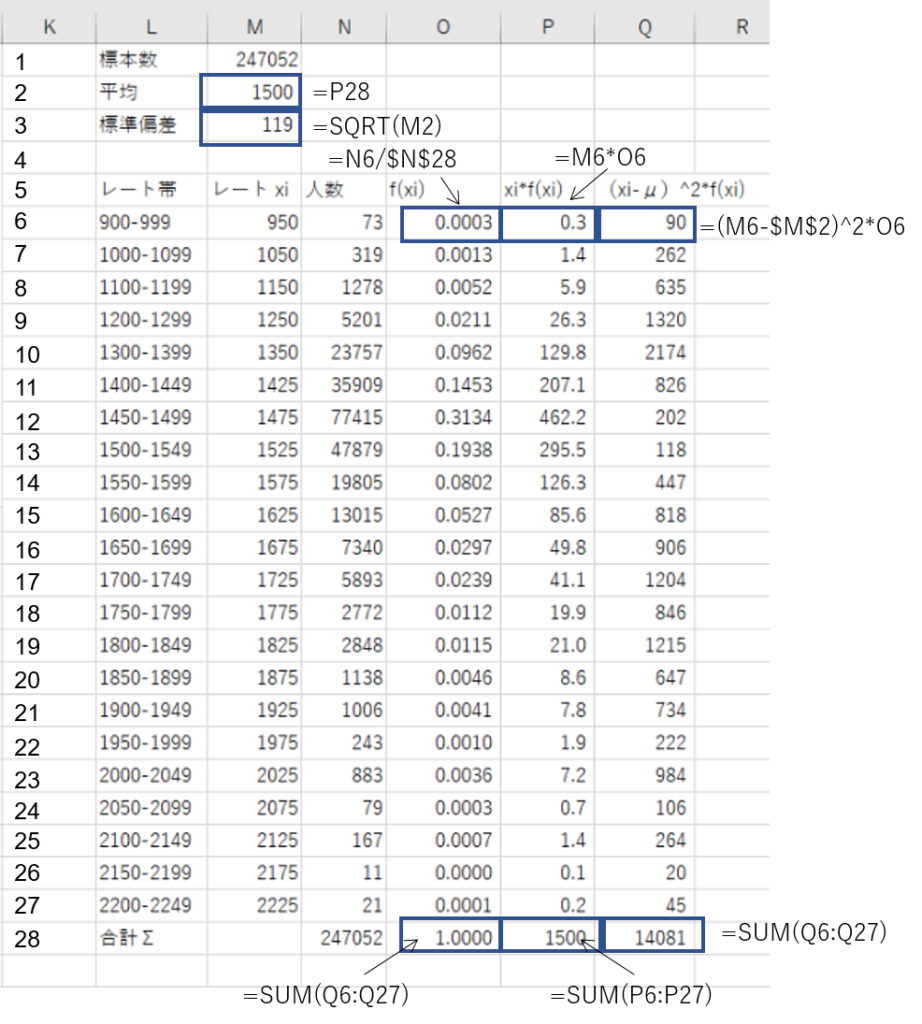
おう。そしたら、平均が1500、分散が14081、それの平方根をとった標準偏差が119だってことが分かるから、以下の式から標準偏差を求められるよな。

なるほど。さっきの表は平均に1500、標準偏差に119を代入して求めたのね。

まとめ

今回は、ポケモンレートと偏差値の関係を示しました。

もちろん、レート帯１４００～１６００の中には、ちょっとだけレートバトルをやって放置している人が大勢いるということは承知しております。（私も最近やってないです。）
これは学力偏差値やTOEICの点数にも当てはまる（全員が全員ホンキで勉強しているワケではない）ことなので、その点含めて偏差値であるという考え方でいいのでは、と思います。