資料請求番号：TS52

熱交換器設計に必要な「対数平均温度差」を導出し、その過程で熱交換器への理解を深める

はしがき

化学工場に必要な機器の一つに「熱交換器」というものがあります。これは物質の温度を調整するのに使用されます。

私たちが普段の生活の中で、モノを温めるのにはガスコンロを使い、冷やすのには冷蔵庫を使用するわけですが、化学工場で取り扱うような、トン単位の物質でこれを行うと非常に効率が悪くなってしまいます。
例えば、ガスコンロや冷蔵庫は、その機器を使用したとき、私たちは「温かい（熱い）」「冷たい」と感じます。我々が機器を使用していて温かい・冷たいと感じるということは、プロセスから見れば、その分だけ熱を棄ててしまっていることに相当するので非常に効率が悪い。と言えるのです。

そこで、物質が持つ熱量を無駄なく上げたり下げたりするための機器としての「熱交換器」が使われています。

「熱交換器」という機器を知るためには、基礎知識として「熱量計算(高校物理レベル)」「伝熱計算(化学・機械工学の初歩)」、そして「微分積分(数学Ⅲ～大学1回生レベル)」が必要になります。

今回は、これらを駆使して熱交換器設計に必要な計算を行い、熱交換器の理解を進めていきます。
その中で、多くの学生が「公式」として使用している「対数平均温度差」の導出および、一般論として「並流よりも向流の方が熱交換効率が良い」と言われている理由を説明したいと思います。

熱交換器の構造

熱交換器の構造を極限までに簡略化した構造が以下のようになります。

この機器には、二重管になっており、２種類の流体を混合することなく流すことができます。
片方の管には温度が低く、温度を高めたい流体を、もう片方の管には温度が高く、温度を下げたい流体を流します。
このようにして、温度の低い流体と温度の高い流体との間で熱量を「交換」するのです。

【重要】熱交換器内の温度分布

ここでの説明は非常に重要です。以後、両流体の熱収支に関する方程式を立てて熱交換器の解説を行っていきますが、その式で使われる文字の説明をこちらで行っていますので、読み飛ばさないようにしてください。

温度が低く、温度を高めたい流体を「低温流体」、温度が高く、温度を下げたい流体を「高温流体」と呼び、「低温流体」の物理量にはC、「高温流体」の物理量にはHの添え字をつけて表現します。
低温流体の流量はW_C[kg/s]、比熱はC_pC[J・kg^-1・K^-1]、
高温流体の流量はW_H[kg/s]、比熱はC_pH[J・kg^-1・K^-1]とします。

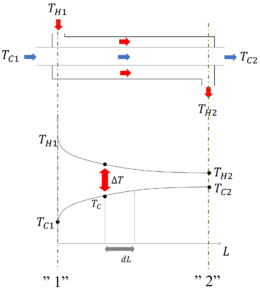
先ほどの、熱交換器の図と熱交換内の低温・高温量流体の温度分布を併せて示すと以下のようになります。

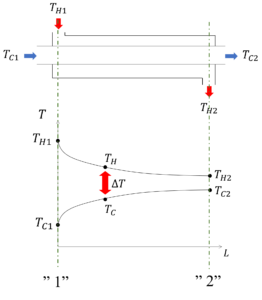
熱交換器を正面に見たとき、向かって左側の配管出入口を”1”、右側の配管出入り口を”2”と表現することにより、

地点”1”を出入りする高温流体の温度をT_H1、低温流体の温度をT_C1、
地点”2”を出入りする高温流体の温度をT_H2、低温流体の温度をT_C2

と置きます。ある地点における高温流体の温度をT_H、低温流体の温度をT_Cと表現し、その温度差をΔTと置きます。

対数平均温度差

この時、上記熱交換器での交換熱量Q[W]は、内管外管間の総括熱伝達係数をU[W・m^-2・K^-1]、伝熱面積をA［m²］としたとき、以下の式で表されます。

この時、ΔT_lmを「対数平均温度差」と呼び、以下の式で表されます。

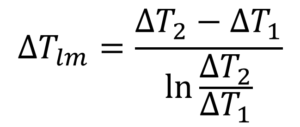
対数平均温度差の限界

初歩的な熱交換器計算は

と熱交換器を通ることで増加または減少した片方の流体の熱量

または

とを合わせて解くことによって、可能になります。これにより、学生は単位を取得することができます。

しかし、実際に熱交換を行うと、

・熱交換器の中で物質の比熱は変化する。
・総括熱伝達係数は内管外管全領域で一定でない。

といった、問題にぶつかることになります。この時、対数平均温度差という公式が使い物にならなくなります。なぜなら対数平均温度差には

「低温・高温量流体の比熱は交換器内で一定」
「総括熱伝達係数は交換器内で一定」

という仮定があるためです。

そのため、本ページでは「どのようにして対数平均温度差が導かれるのか」を数式で追及しつつ、「上記２つの仮定がどこで使われ、その仮定が打ち破られるような熱交換器の場合、どのように設計したらいいか、を考えていきます。

低温流体・高温流体の熱収支式

計算の方針

低温・高温両流体が、熱交換器内の微小区間dLを通過するとき、

高温流体はどの程度の熱量を失い、
低温流体はどの程度の熱量を獲得するのか、

を計算します。

熱交換器の概略図と温度プロファイルを利用して、高温流体が失う熱量と低温流体が獲得する熱量を求めると以下のようになります。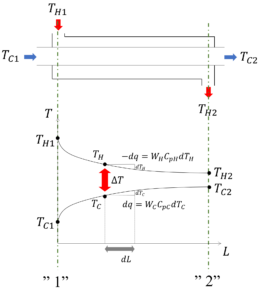

ある微小区間dLにおいて、高温流体はdT_Hだけ温度が下がり、低温流体はdT_Cだけ温度が上がる。そのとき、dqだけ熱量が交換され、dqは以下のように表されます。

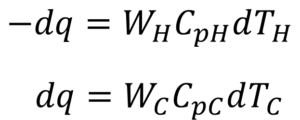
交換熱量と温度差

dqの値は、低温高温両流体間の温度差が大きいほど大きくなります。
dqの単位は[W]、すなわち[J・s^-1]です。熱が移動する「速さ」を表しているのです。
物質・熱・運動量が移動する速さは、その勾配が大きいほど大きい、という移動現象論の基本原理に則って考えると、伝熱速度dqは以下の式で表されることが推測できます。

dq=k(T_H–T_C)

ここで、定数kについて考えます。

※参考
[blogcard url=”http://shimaphoto03.com/science/transport-phenomena/”]

総括熱伝達係数U

再度、確認を行いますが、現在行っていることは、「二重管式熱交換器の微小区間dLにおいて、内管と外管との間で交換される伝熱速度dq[W]の計算」です。

伝熱速度dq[W]は
①内管と外管を隔てる配管の素材
②内管と外管を通る流体の流速
③内管や外管の汚れ具合
などの要素によって変化します。

①について、これは一般的に言われる、
プラスチックよりも鉄の方が熱を通しやすい
という事実に対し、どれだけ熱を通しやすいのかを熱伝導率と呼ばれる数値で数値化した値を使用します。

②について、45℃くらいの熱いお湯に水を入れ、それを手でかき混ぜることによって「いい湯」にすることをイメージしてください。
この状況で、手で早くかき混ぜればかき混ぜるほど「熱い」と感じると思います。このことを専門用語を使って「手を早く動かすことにより、手からお湯にかけて形成される境膜が薄くなったため、伝熱速度が増した。」と表現します。
この現象と同様に、内管と外管を通る流体の流速が速ければ速いほど境膜が薄くなり、伝熱速度は増加します。
境膜について説明しだすと1記事レベルになってしまうので、「伝熱抵抗の一つ」くらいに考えていただければ結構です。

③について、配管にスケール（いわゆる水垢みたいなもの）が付着していると、本来
高温流体→配管→低温流体　で熱が伝わるところ、
高温流体→配管の汚れ→配管→配管の汚れ→低温流体　で熱が伝わるので、
伝熱速度が落ちてしまいます。

このように、内管と外管のコンディションによって、伝熱速度が変化します。内管と外管との間の伝熱速度に関係する因子を挙げて、それを全て総括して表現したのが、総括熱伝達係数U[W・m^-2・K^-1]です。

具体的にどのように総括し、Uを求めるか、というのは、電気工学でいう「抵抗値の和をとる」ことと同じことをしているのですが、ここも説明しだすと長くなってしまうので、割愛します。

伝熱面積A

伝熱速度は、内管と外管との間のコンディションに加え、伝熱面積で決まります。つまり、

dq = UA(T_H–T_C)

なのです。
ただし、現在は、熱交換器の微小区間dLについての伝熱速度を考えているので、
A = πDL（Dは配管径）より
dA=πDdLとなります。以上より、

dq=UπDdL(T_H–T_C)

となります。

基礎式の完成

熱交換器の微小区間dLでdqの伝熱速度で熱交換が行われるとして、dqについて

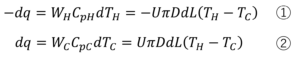
の２式が完成します。以後、この式を式変形していきます。

式変形と対数平均温度差の導出

ステップ１

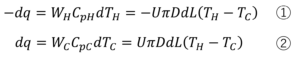
①、②の２式をdT_H,dT_Cで表すと

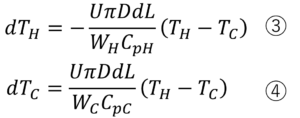
以上の③、④式となります。
③-④式より⑤式が得られます。

ここで、式変形を行いやすくするため、

と置きます。
よって、⑤式は以下のように簡略化できます。

⑥式は独立変数をL、従属変数をΔT(L)としたときの常微分方程式です。
これを境界条件ΔT(0)=ΔT(ΔT₁)、ΔT(L)=ΔT(ΔT)として解きます。

ここで、注意しなければならない点として、K,UおよびDは、Lの関数ではなく定数であるという仮定のもと、∫から外してしまっている点が挙げられます。
「低温・高温量流体の比熱は交換器内で一定」
「総括熱伝達係数は交換器内で一定」
という仮定があるから、このような式変形が実現することに注意します。
例えば、比熱が一定でなければ、比熱を温度の関数C_p(T)として表現したり、総括熱伝達係数が一定でなければUをU(L)として表現し、積分計算する必要が出てくるでしょう。

ステップ２

次に、微小区間dLを低温流体が通過したとき、低温流体が得る熱量に注目して

を式変形していきます。
上式は

ですので、⑧式より

これを0~Lまで積分すると、熱交換器のある地点Lまでの総交換熱量Qが取得できます。

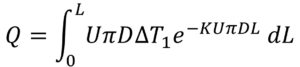
「低温・高温量流体の比熱は交換器内で一定」
「総括熱伝達係数は交換器内で一定」
という仮定から

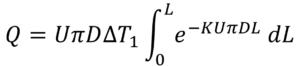
となりますので、

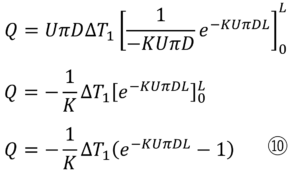
ここで、Kは⑦式を変形した

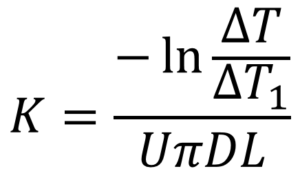
で表現できるので、⑩式へ代入して

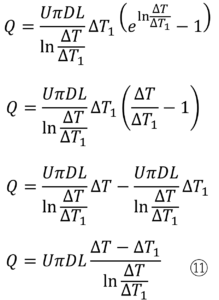
⑪式について、積分終了地点を”2″と定め、ΔT＝ΔT₂とすれば

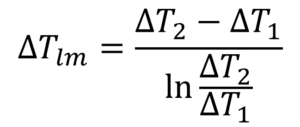
のようにΔT_lmが得られ、これを「対数平均温度差」と呼びます。よって、熱交換器全体の交換熱量Q[W]は

と表されます。

並流よりも向流の方が熱交換効率が良いといわれる理由

ステップ２において、微小区間dLにおける伝熱速度dqは以下の式で表され、

これを0~Lまで積分すると、地点Lまでの総熱交換量になることを説明しました。つまり

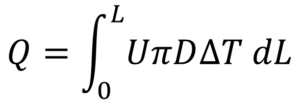
ということになります。
以上より、「並流より向流の方が熱交換効率が良い理由を説明せよ」という問題は、
「並流よりも向流の方が

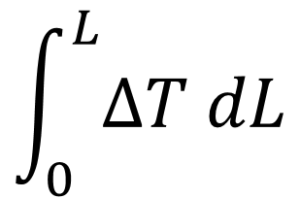
の面積が大きい理由を説明せよ」
という問題に書き下すことができ、

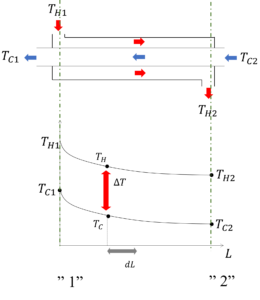
この図における

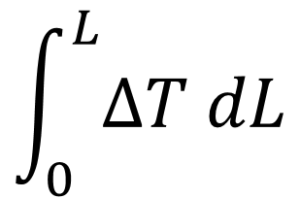
の方が、

この図における

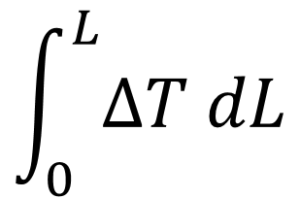
の面積よりも大きいことを説明できれば良いのですが、

「見た目でわかる。」と言ってしまえばそこまでです。

熱交換器において、

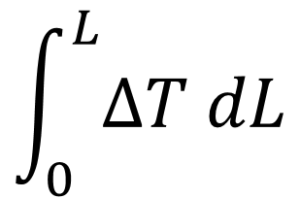
が大きい操作条件において、大量の熱を交換できる。という感覚を身に着けておくべきなのかな。と思います。

伝熱と呼ばれる現象は温度差を駆動力として起こる現象であるということが分かっていれば、上記の積分と熱交換量の大きさの関係がより理解しやすいかと思います。

まとめ

今回は、熱交換器設計に必要な計算を行い、熱交換器の理解を進めていきました。

その中で熱交換器の熱収支式を立て、その常微分方程式を解くことによって、ある地点Lにおける高温流体と低温流体の温度差ΔTを求めることができようになりました。さらに、熱収支式から対数平均温度差を導き出し、対数平均温度差が導出される際の「仮定」について考えました。

対数平均温度差が使えないような自然現象やプロセスを取り扱う際には、熱収支式の基礎式に立ち返って、自分で式を作らなければなりません。複雑な構造や複雑な現象を応用した熱交換器の登場により、対数平均温度差を知っていればよい、というわけにはなくなりました。そこで、いかにして「対数平均温度差」が出てきたかを考えるのが非常に重要だと私は思います。