資料請求番号:TS35
スポンサーリンク偏差値は統計に基づいた指標である
メリークリスマスでございます。世の中の人々が現を抜かしている中、受験生は勉強に勤しんでいるかと思います。
センター試験も近づいてきましたね。
今回は、偏差値のお話をしたいと思います。偏差値。それは受験生の多くが意識したことのある数値だと思います。
偏差値という数字は数学的にどのような意味を持つのか?そして偏差値の計算方法は?
といった疑問にお答えしたいと思います。
偏差値のイメージ

ねぇ、ストーク。こないだ、全社員統一学力試験の結果が出たじゃない?

あぁ、ウチの会社の正社員全員が受ける学力試験のことか。ウチの会社もえげつないことするよなぁ~。なんであんなことするんやろな。
コストもバカにならんたいね。

う~ん。なんだかんだ言って、社会人も勉強は大切ってことなんじゃないかしら?数学は別にsinやcosが使えなくても、せめて割合の計算くらいはできないと仕事にならないし、国語は敬語の使い方が毎年出るでしょ?これがしっかりしていないと社会人として恥ずかしいしね。
受験勉強の模試とは違って、社会人として、あるいはメーカーで働く者として必要とされる知識を試されている気がする。

確かにな。数学は毎年、必ずと言っていいほど平均や分散を求めるみたいな統計の問題が出るしな。ウチは製紙メーカーやし、統計学の考え方は品質管理(QC)において非常に重要たいね。

それでこの試験の成績表にある偏差値って言う項目、どうやって計算されるの?言葉だけは知ってて受験期はよく使った言葉だけど、ワタシ、ちゃんと理解してないな~と思って。なんか、偏差値と統計学が関係しているって言うのは聞いたことがあるんだけど、具体的にどういう考え方でどういう計算方法なのかは分からないのよね~。

そっか。偏差値は一言でいうなら、「その人の点が、みんなが取る点よりも、どれだけズレているか」を示す指標だ。偏差値は以下の式で定義されている。


あ、確かに。平均からの差をとっているね。この標準偏差って言うのは・・・確かデータのバラツキを表す指標でしょ?

そうそう。この標準偏差が大きいほど、データがバラついている。試験で言うならば、得点が0点から100点まで幅広く分布しているということたい。
一方、標準偏差が小さいとデータはある数値に密集している。試験で言うならば30点台の人がメチャクチャいて、他の点数の人は全然いないというような状態。
例えばこんな試験で80点とか90点とか取ったらどうだ?

え?30点台の人が多い中、80点とか90点とか取ったら・・・スゴイわよね。とても優秀よね。

これが「みんなが取る点よりもとっても高くズレまくっているから優秀」ということなんだ。
その優秀さってのを数字にしたもの偏差値になって現れるわけだ。ホラ、偏差ってズレを意味する言葉やろ?
30点台の人がメチャクチャいて、他の点数の人は少ないような試験は標準偏差が小さい。分母が小さいから偏差値は大きくなりやすい。

なるほど・・・。

今回の全社員学力試験では標準偏差の大きい試験が数学、小さい試験が国語だった。成績表に添付されている得点分布表をみてみろ。
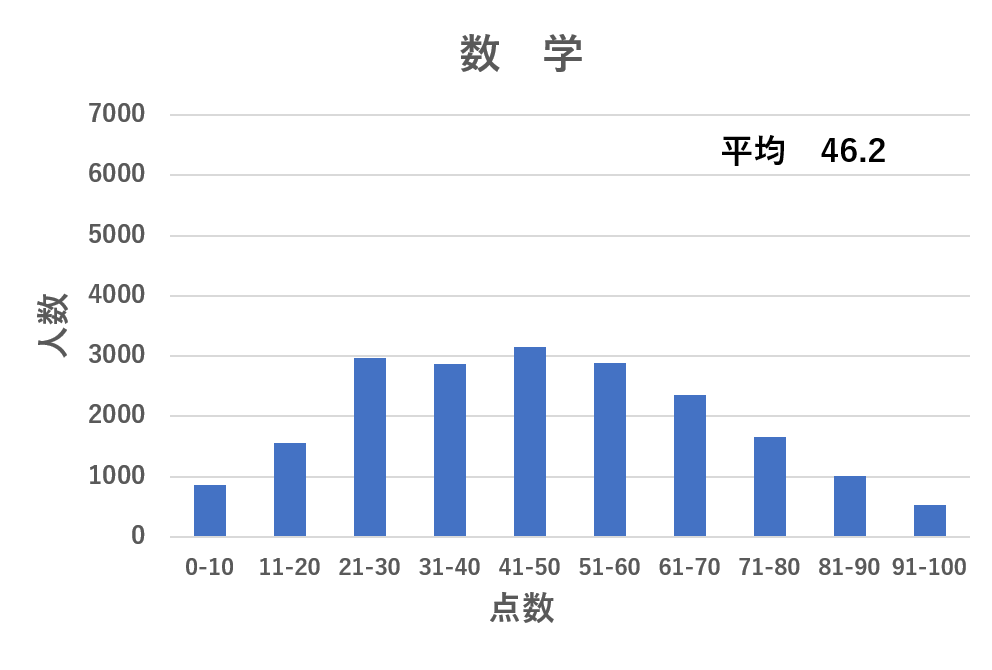
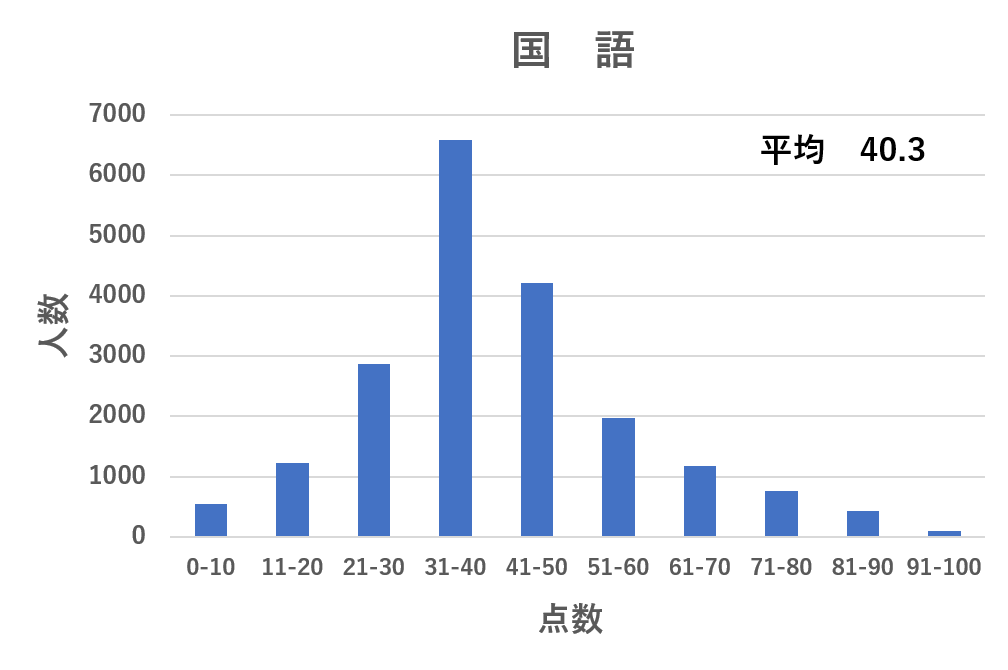

あ・・・確かに。

俺は数学の試験で96点をとった。偏差値は72.3だ。
しかしディープルは国語の試験で90点をとっていて、偏差値は79.6だそうだ。
点数自体は96という俺の数字の方が大きいのに、偏差値が俺の数学よりディープルの国語の方が高いのは、標準偏差が小さいからだ。
数学における右端の人と、国語における右端の人。どっちが優秀かといえば後者やろ?

なるほど~!だから標準偏差っていうバラツキの指標が偏差値においては大切で、計算式の中に含まれているのね!

・・・っていうか、今年の国語の試験、難しかった~。

ああ。俺は42点だった。初めてだよ。50点以下とったの。
最初は敬語や漢字の問題とか、契約書や特許の読解問題とか出されてて、いつもの試験と同じやろ思てたら、いきなり古文漢文とか出てきやがったからな~。うったまがったい。

うったまがったい??

ああ、熊本弁でビックリしたって意味。

何であんな問題だしたのかしら?それにディープルすごすぎよ・・・。

ディープルが言うには、古文漢文に出てくる話って言うのは、「物事をあまり深く考えすぎてはいけない」とか、「心配事を追求しても仕方がない」とか、
そういう「気持ち」の面で勉強になるから、うつで引きこもった時に勉強していたそうだ。
最近は、メンタルヘルスが全社的に問題になっているから、古文漢文も勉強してみたら?という出題者のメッセージかもしれんたいね。

そっか・・・。
偏差値は
・平均との差
・標準偏差の大きさ
で決まります。この二つの数値を使って「その人の点が、みんなが取る点よりも、どれだけズレているか」を表す指標なのです。
平均との差が大きいほど偏差値が高いというのはイメージわきやすいかもしれませんが、標準偏差はイメージわきにくいかもしれません。
標準偏差とはデータのバラツキ具合を示す指標で大小さまざまなデータが広く分布しているとこの数字は大きくなります。
試験の話で言うならば0点~100点の人が幅広くいる場合、標準偏差が大きくなります。
0点~100点と、色々な人が存在するような試験で高い点数をとっても、「みんなが取る点よりも、そんなにズレない」ため、偏差値は大きくなりにくいのです。
逆に、ある点数、例えば30点台の人が密集しているような狭い分布だと、バラツキが小さいので標準偏差は小さくなります。
このような試験で90点をとれば「みんなが取る点よりも、大きくズレている」ので偏差値が大きくなるのです。
標準偏差の計算
では、データのバラツキ具合を示す標準偏差はどのようにして計算されるのでしょうか?標準偏差は以下の式で表されます


じゃあ、この式を使って、標準偏差を出す練習をしてみようぜ。
今回の数学の試験の4人の成績は以下の通りだった。


これの標準偏差をシママ、求めてみろ。

標準偏差の計算は、今回の数学の試験問題にも出たから大丈夫。まずは平均を求めて
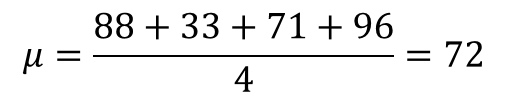

それから、それぞれの平均値との差を出して、それぞれ2乗するのよね。2乗したものを全員分足し合わせる。
そして、これを標本数、今回は4ね。4で割れば分散が出てくる。
標準偏差は分散の平方根ね。
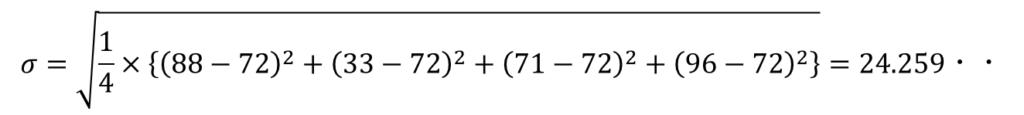

標準偏差は24.3!

そうだな。Excelシートでこんな感じに計算すればいいだろうな。
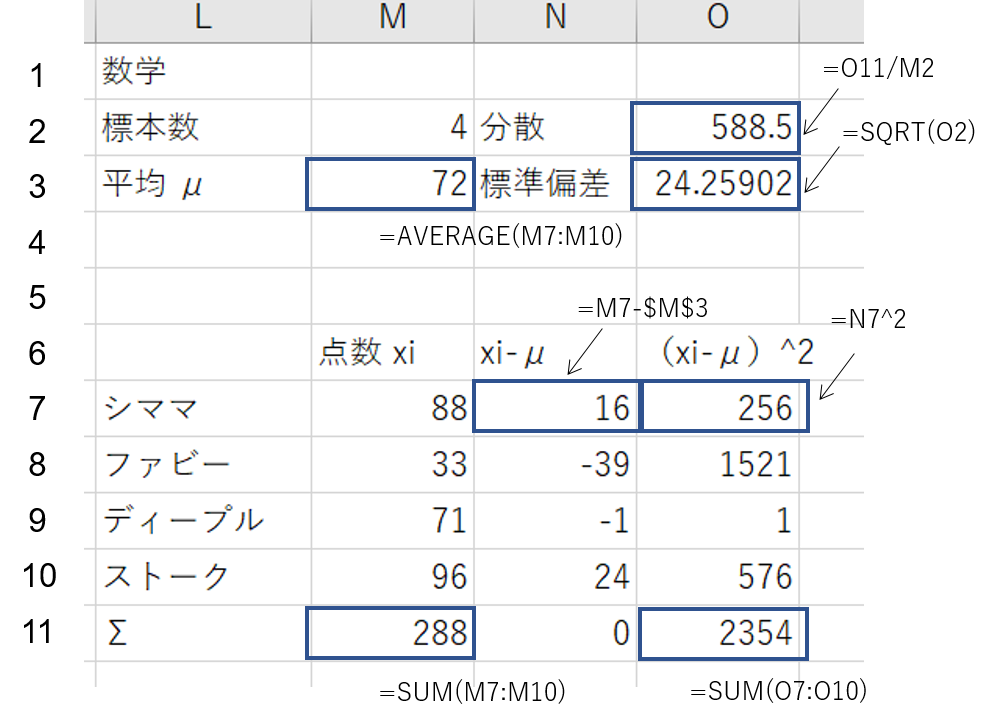

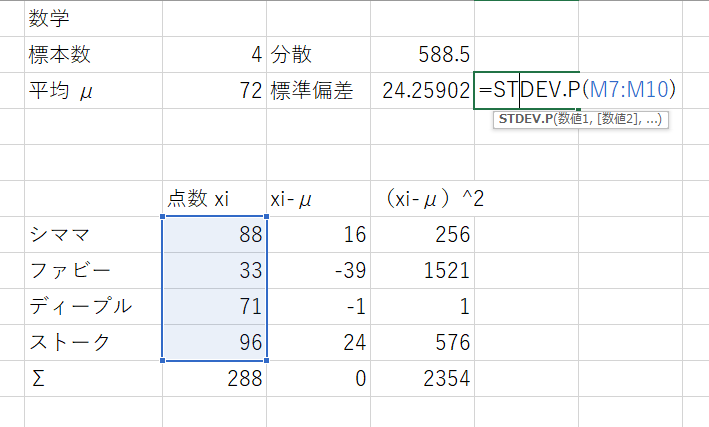
Excel使うんだったら、STDEV.P関数を使えばいいんだら?

そうそう。それ使えば一発で標準偏差は出せる。これでエンター押せば標準偏差24.3が出る。

よし。じゃあ次、社会の点数は以下の通りだった。標準偏差は?

・・・・

平均が65.3、標準偏差は5.36ね。
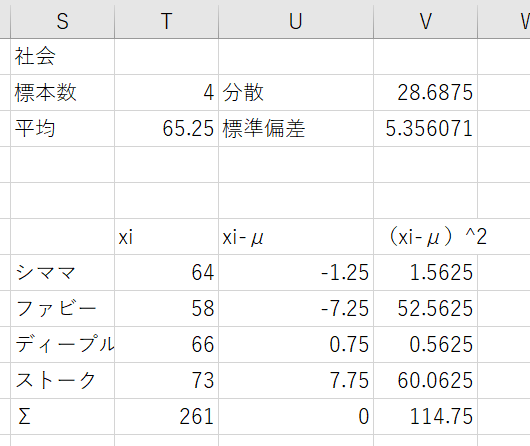

その通りだ。数学と社会で、4人の点数と標準偏差を見比べてみろ。

あ~・・。33点から96点まで幅広く分布している数学は標準偏差高くて、
58点から73点という、比較的狭く分布している社会は標準偏差低いのね。

試験では計算式に当てはめて計算するだけだったけど、実際のデータと標準偏差の関係が結びついた気がする!

そっか。それは良かった!
得点分布から平均と標準偏差を計算する

これさぁ、ヒストグラム(得点分布表)から平均点を求めたり、標準偏差を求めてそこから自分の偏差値を出したりできるのかしら?

あぁ、概算だができるぜ。それ出来たら社員約2万人の点数を知らなくても偏差値を概算できるよな。

うん。そうなのよ。ヒストグラムだけ与えられて平均とか標準偏差とか偏差値を知りたいという場合もあるかもしれないじゃない。

この場合はな、点数を変数xi、ヒストグラムの高さをxiの関数f(xi)に見立てるんだ。このとき、xiを確率変数、f(xi)を確率密度関数という。今回の場合はそうだな・・・0-10点の点数を5点と近似しようか。
そうしたときに今回の数学の点数とそれを取った人数の関係は以下の様になる。
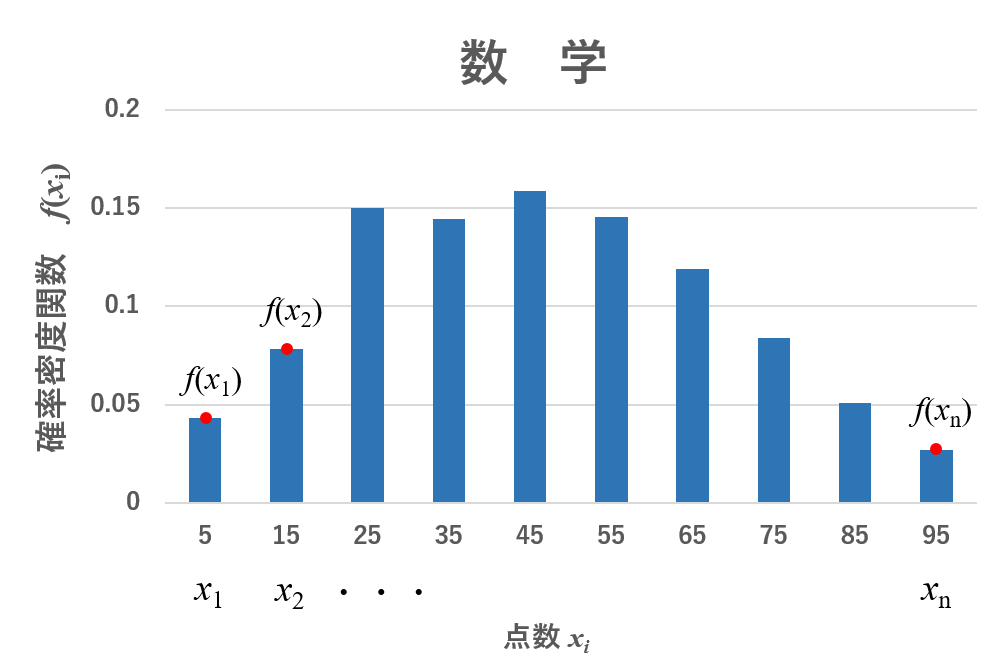
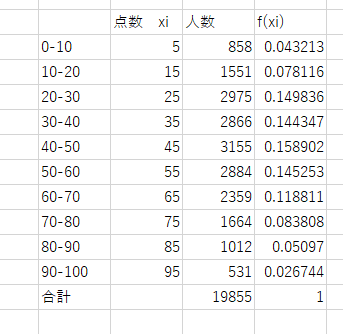

あれ?縦軸の数字って・・・?どうやって計算するの?

それぞれの変数xiにおける人数の和を取ると、受験者数19855になるだろ?
一方で、確率って言うのは、全事象の和が1になるものだ。だから、人数を受験者数で割るんだ。
そしてできるのが確率密度関数f(xi)だ。この作業を正規化という。

なるほど・・・。

こうしてできた確率変数xiと確率密度関数f(xi)から、平均μと分散σ2が以下の式で求められる。
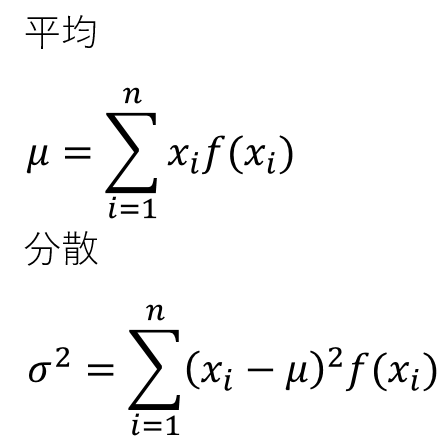

これで平均μと分散σ2と標準偏差σを計算してみろ
・・・・

こんな感じ?
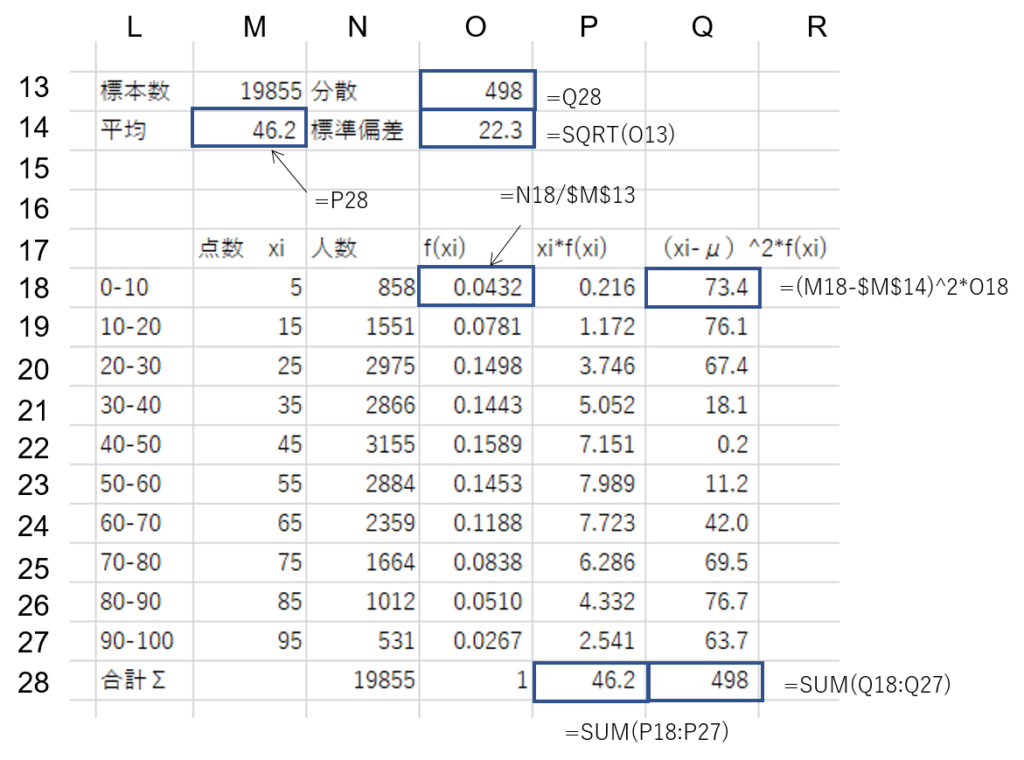

そうだ。これで自分の偏差値が概算できるだろ?


あ~、確かに!
ある値の範囲が出た回数(頻度)をその値の関数に見立てると数学的な処理ができるようになります。
このような手法はテストの点数の分布だけでなく、粉体の直径の分布を解析するなど、モノづくりの世界においても応用されています。
確率密度関数は全範囲にわたって積分すればその値が1になるよう正規化されています。
正規分布と偏差値
確率密度関数はある値とその値の頻度の関係を関数に見立てたものですが、これまでの計算だと、この関数は連続しておらず、数学的処理が難しくなります。従って、連続したある関数に近似することでさらに数学的な解析を可能にします。
今回のケースのように、2万人という十分に多い標本に対して、試験を行うと、その試験の得点分布は正規分布に近づくといわれています。正規分布とは
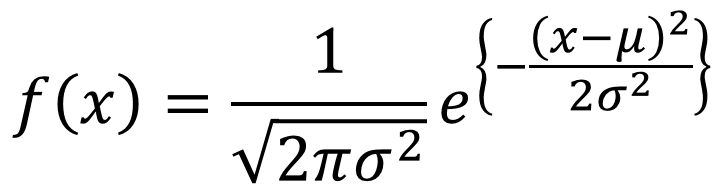
で表される山のような形をした関数で、平均が50点、標準偏差が10の場合、20の場合の正規分布は以下のような形をとります。
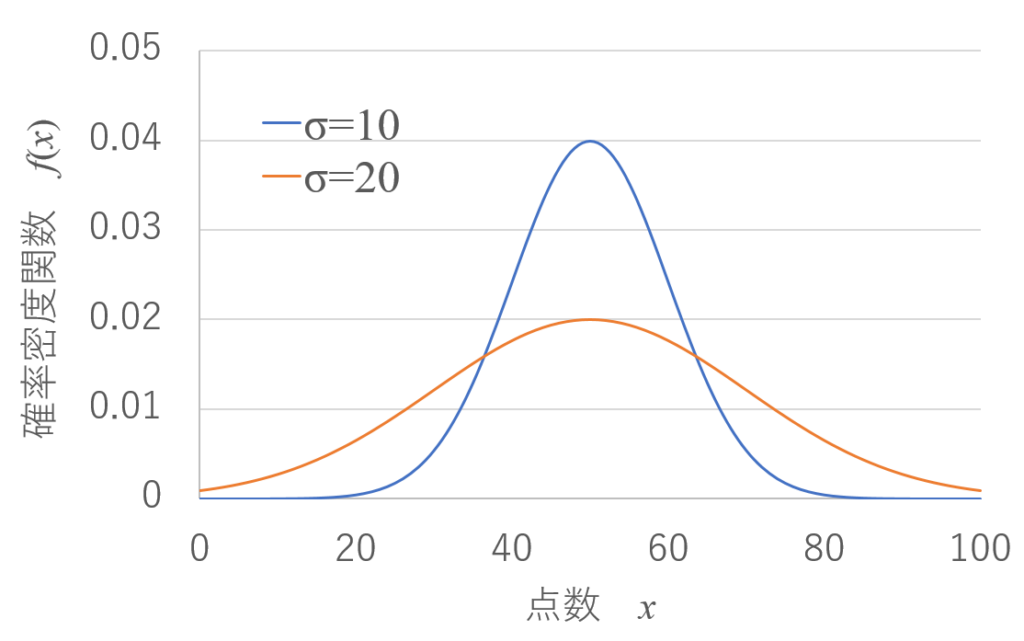

この正規分布は平均をμ、標準偏差をσとしたとき、μ–σから、μ+σの範囲で積分すると0.683、μ-2σから、μ+2σの範囲で積分すると0.955、μ-3σから、μ+3σの範囲で積分すると0.997になるたい。
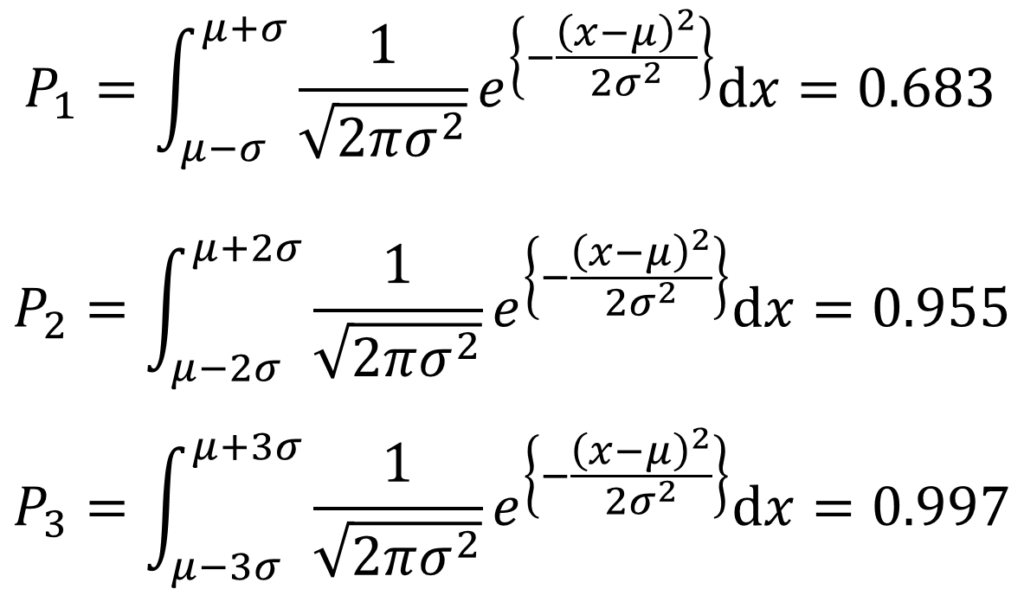

???

つまり、平均50点、標準偏差10の試験においては、40点~60点を取る人が68.3%いるということになるんだ。

あ~なるほど・・・。確率密度関数を積分すれば、その積分範囲の数値をとる確率がでてくるのね。

あ、これもしかして、-∞から∞まで積分すれば1になる?

その通りだ。じゃあ、このような平均50点、標準偏差10になった試験において、60点を取った人の偏差値は?

え~っと・・・偏差値の定義はこうだから・・・。
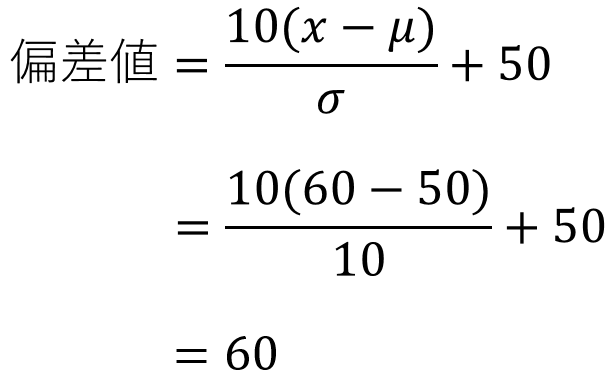

あ、60だ。というか、この試験なら点数がそのまま偏差値になるのね。

そうなんだ。現実にはいろいろな平均点といろいろな標準偏差があるから、上の式を使って実際の点数から偏差値を計算するんだ。
例えば、今回の数学の試験では、平均点が46.2で標準偏差が22.3だったな。これを正規分布に当てはめれば、こんな感じの曲線になる。
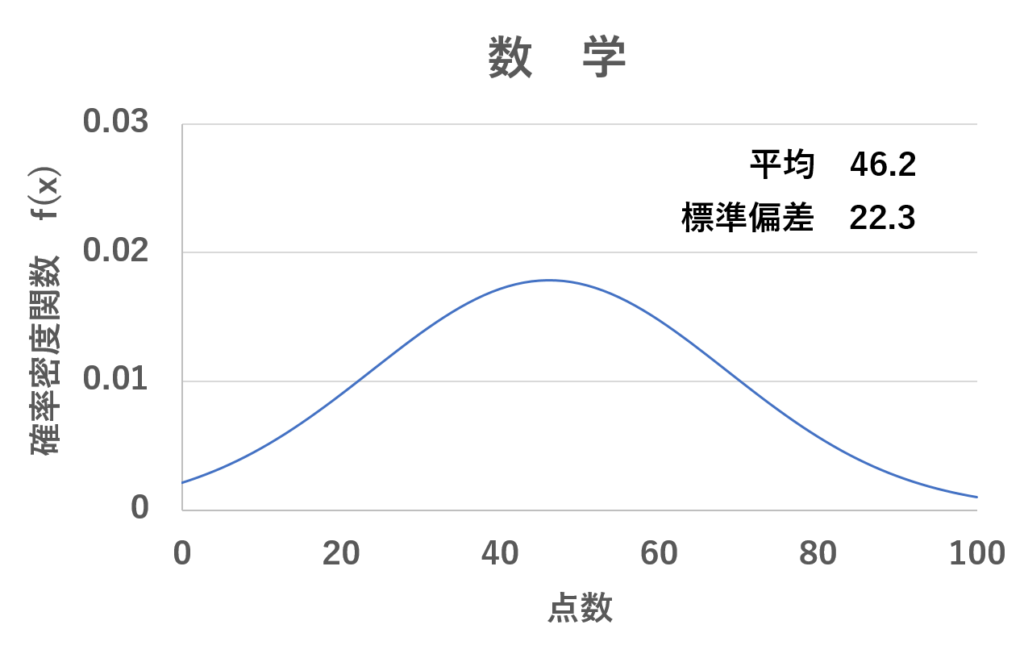

そして、μ–σ=23.9点からμ+σ=68.5点を取る人は全体の中で68.3%になるよな?
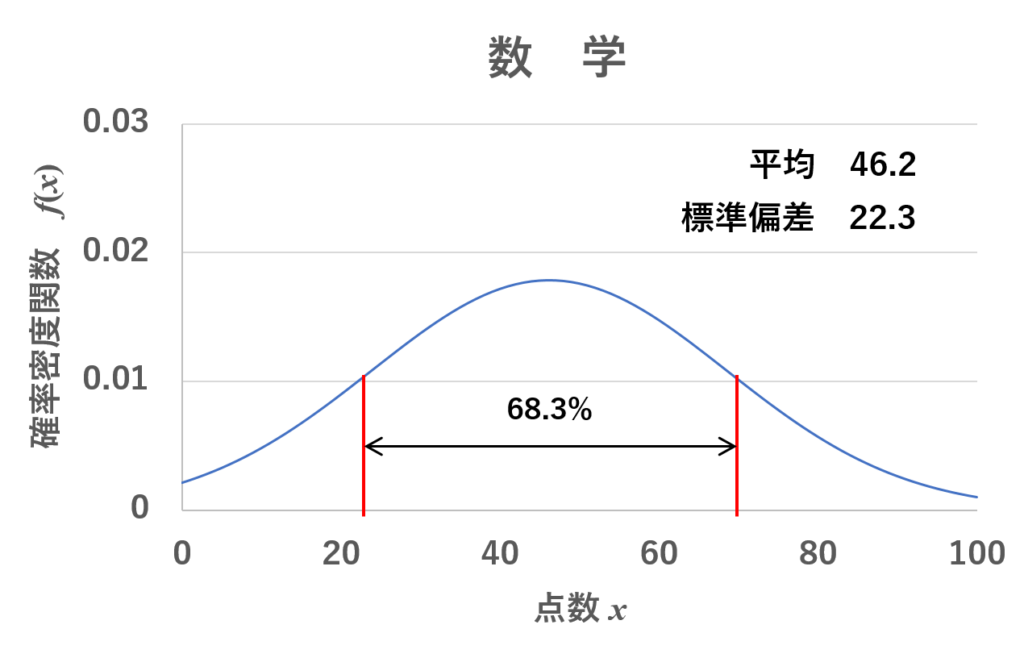

うん。そうね。正規分布は平均をμ、標準偏差をσとしたとき、μ–σから、μ+σの範囲で積分すると0.683になるからね。

それで、23.9点の人の偏差値と、68.5点の人の偏差値を計算してみろ。


あ、40と60になった。そっか!偏差値って点数が1σ減ると10減って1σ増えると10増えるんだ!
そうなるようにこの偏差値の定義があるのね!

その通り!偏差値が分かれば、自分が上から大体何%かっていうこともわかるんだ。

え?じゃあ、ディープルが国語でとった偏差値79.6・・・偏差値約80ってかなりヤバいんじゃ・・・。

ああ、ヤバいよ。μ-3σが-10.1点、μ+3σが90.7点だ。この範囲の中に99.7%が収まることになる。それで、90点をとったディープルは偏差値79.6でこの範囲ギリギリに収まる。つまりヤツは上位0.3~0.4%くらい、1000人に3人か4人くらいの成績を出したわけだ。
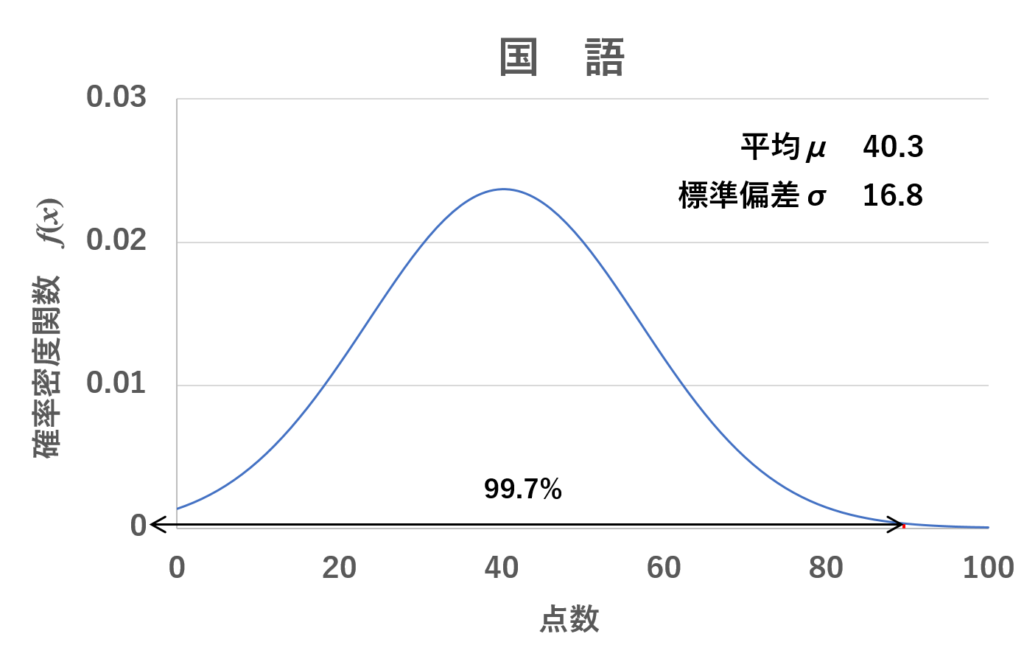

いや~すごいのね~。尊敬するわ~。しかもあの子、地味に数学の点数も高いしね。71点でしょ?ってことは、数学のμ+σは68.5だから偏差値60越えてるわよ。
学卒含めてこの成績よ?

ヤツは学習能力がハンパなく高いからな。そこんとこは学歴とあんま関係ない気がするな。

・・・結構、自己を見つめる良い試験なのかも。

そうかもな(笑)。人事にとっても、隠れた才能を発掘するのに使えるのかもな。
まとめ
今回は、偏差値をテーマに、
・偏差値の出し方と偏差値のイメージ
・標準偏差の計算方法
・ヒストグラム(分布)が与えられた時の平均と標準偏差、偏差値の計算方法
・偏差値と正規分布の関係
についてだんだん数学色を出しながら解説していきました。
「偏差値」でgoogle検索すると「偏差値100」というワードが出てくるのですが、偏差値100が出るのはほとんどないか、非常に条件が良かったときのみということがわかるでしょう。また、偏差値80の凄さというのもお分かりいただけたかと思います。
勉強においては全体における自分の立ち位置を知ることは大事ですが、それに囚われ過ぎると却って足かせになることがあります。
偏差値はあくまでついて回るものと考えましょう。
勉強あるのみです。勉強した結果、偏差値が自然とついてくるという感覚で勉強したほうが捗るかと思いますし、精神的にもラクです。
それでは、センター試験を控えている人を含め、受験を控えている人は頑張ってください。
インフルエンザにはご注意を!頑張ることは大切ですが、ご自愛ください。
 らい・ぶらり
らい・ぶらり


コメントを残す