資料請求番号:TS13 TS14 TS51

う~ん・・・。物理や化学って難しい。

どんなところが難しいと思うんだ?

だって、公式をたくさん覚えなくちゃいけないでしょ?
それに覚えたって、いざ問題を解くときになったら、どの公式を使えばいいのか分からなくて頭がこんがらがっちゃって・・・

公式・・・か。ファビーさ、学校で教えられる公式の右辺と左辺は必ず単位が一致するっていうことを意識しているか?

いや、まったく。

単位を意識して計算しようとすると、物理や化学の計算が一気に捗るぜ。
今回はその方法を教えてやるよ。
計算をわかりやすく簡単に進めるために
「単位を使う」
という考え方を取り入れてみましょう。それでは詳しく見ていきます。
学校で教えられる計算方法
こんな記号を教えられた経験はありませんか?
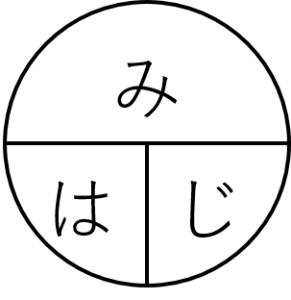
「みはじ」っていうのはそれぞれ「道のり」「速さ」「時間」を表しますよね。そしてこの記号を見て
道のり=速さ×時間
速さ=道のり÷時間
時間=道のり÷速さ
という公式を思い出しながら問題を解いていきます。

これ、単位と一緒に考えてみるぜ。
道のり(km)=速さ(km/h)×時間(h)
「km/h × h」はkmになるだろ?右辺と左辺は単位が必ず一致しているんだ。
他にも
速さ(km/h) = 道のり(km) ÷ 時間(h)
時間(h) = 道のり(km) ÷ 速さ(km/h)
全部一致してるだろ?
あと、
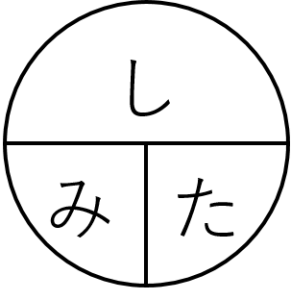
も同様ですよね。
質量=密度×体積
体積=質量÷密度
密度=質量÷体積
ですよね。小中学生の頃はこの方法でいいかもしれません。
私もしょっちゅうこんな記号を書いて問題を攻略していました。

小中学生の計算ではこの攻略法でいいかもしれない。
でも、高校生レベルほど問題が複雑になってくると、
「覚えきれない」とか「何の公式を使って解いたらいいか分からない」っていう悩みが出てきてしまうんだ。
公式を覚えたり、図案化したりするやり方にはいつか限界がやってくるのです。
私はもうすでに上記に書いたような図は使っていません。公式をすべて暗記しているわけではありません。でも、状況に応じて必要な式を頭から引っ張り出して問題を解いています。そこで使っているのが「単位」です。
単位も一緒に計算しよう

じゃあ、具体的に単位を使って問題を攻略していこうぜ。
例えば
「時速40kmで3時間走ったときに進む距離を求めよ。」
という問題があるとしたら
「みはじ」方式なら
①道のりを聞かれているから「道のり=速さ×時間」という公式を思い出す
②公式に当てはめる
(速さは40で時間は3だから40×3=120だ。)
③120kmという答えを導き出す
という思考のプロセスを踏みます。
単位も一緒に計算する方式なら
①求められているものの単位を把握する。

距離を求められているということは?求めるべき答えの単位は?

kmだね!
②問題に与えられている数字の単位を挙げてみる

40km/hと3hが問題に与えられている。つまり、俺らはkm/hとhの情報を持っているんだ。
③「km」になるには「km/h」と「h」をどう組み合わせればいいか考える

kmを出すにはkm/hとhをかければいいってこと?

そう!そういうことだよ!
④答えを求める

40km/h × 3h = 120kmだから、答えは120kmだ!
といった思考のプロセスを踏みます。
一見して後者の方が複雑そうな気がしますが、問題が複雑になった時、公式を忘れてしまったときに威力を発揮します。
単位を使って計算すればミスが防げる
「質量100kgで密度8g/mLの物質があります。この物質の体積は何mLですか?」
という問題があったとします。

体積=質量÷密度という公式で考えると100/8=12.5 mLだと答えてしまいそうじゃないか?でも、この答えは違うよな?
単位を使って計算すれば
①求めたい単位「mL」を出すには「kg」を「g/mL」で割れば良さそうと考える
②「kg」は「g/mL」で割れないことに気づく
③「kg」を「g」に直して計算する
(100kg=100000g →100000 g ÷ 8 g/mL = 12500 mL)
④正しい答え12500 mLを得る。
という思考のプロセスを踏んでミスなく正しい答えを出せるようになります。
単位を使う計算方法は色々なところで使える
これまで「道のり、速さ、時間」と「質量、密度、体積」を挙げてきましたが、それだけにとどまらず、あらゆるところで単位は活躍します。例題とともにそのことを示していきます。

その前に単位を使った計算方法をもう一度おさらいしようぜ。
①与えられた情報の単位をすべて洗い出す。
②求められている情報の単位を考える
③単位どうしを計算させて②で出した単位になる組み合わせを考える
④単位と一緒に数値を計算して答えを出す
例題
問1. 「分子量18の水が180gだけコップの中に入っている。この水のモル数はいくらか?」
①分子量18 → 18g/mol, 180 g
②モル数→必要な単位はmol
③molを出すには「g」を「g/mol」で割ればいい
④180g÷18g/mol = 10mol 答えは10mol
問2. 「濃度0.1mol/Lの塩化ナトリウム水溶液がある。この溶液300mLの中に含まれる塩化ナトリウムの質量はいくらか?ただし、塩化ナトリウムの分子量は58.5である」
①0.1mol/L,300mL,58.5 g/mol
②質量→必要な単位はg
③gを出すには「mol/L × L × g/mol」で出せそう。300mLは0.3Lに換算しておこう
④0.1mol/L × 0.3L × 58.5g/mol = 1.755 g 答えは1.755 g

あ!なんだか化学の問題が解けそうな気がしてきた!
まとめ
公式を忘れてしまった!どんな公式を使えばいいのかわからない!といったときには単位も一緒に計算してみましょう。そしたら解法が見えてくることが多いです。
 らい・ぶらり
らい・ぶらり


コメントを残す