資料請求番号:TS39
スポンサーリンク座標変換の公式導出の考え方
高校数学Ⅲでは、2次元で極座標変換して円や楕円・カージオイド・アステロイドなど、「丸いもの」の式を求めたり、概形を描いたりする問題が出題されます。
東北大学の過去問にはリマソン(蝸牛線)と呼ばれる図形を対象に極方程式を求め、その概形を描いたり、最大最小を求めたりする問題がありました。
大学に行った後も、物理現象の解析をしていると、3次元の極座標(球座標)変換という概念が出てきます。
というのも、点電荷のように球状に電場をつくるようなモノがあったり、温度は四方八方に伝わっていくように、球で表現したほうが都合の良い物理現象が多いため、3次元極座標というものは現象の解析に欠かせないものとなっています。
ところが、3次元の極座標と直交座標の関係式を導出せよ。という問題に当たったとき、慣れていないと少し混乱します。
解き終えれば「何でこんな簡単なことも分からなかったんだ?」と思うくらい簡単な問題ではありますが、初見では混乱します。(少なくとも私は混乱しました。)
対象が3次元であるため、紙に書いてある図から3次元の座標などを想像するのが難しいのです。
本記事では、極座標と直交座標の変換公式の導出ということで、3次元極座標のイメージを説明したのち、
なるべく頭の中で直交座標と極座標の関係がイメージしやすいように図を多用してじっくり導出してみました。
問題の例
極座標で定義された点(r,θ,φ)を直交座標系(x, y, z)で表せ。
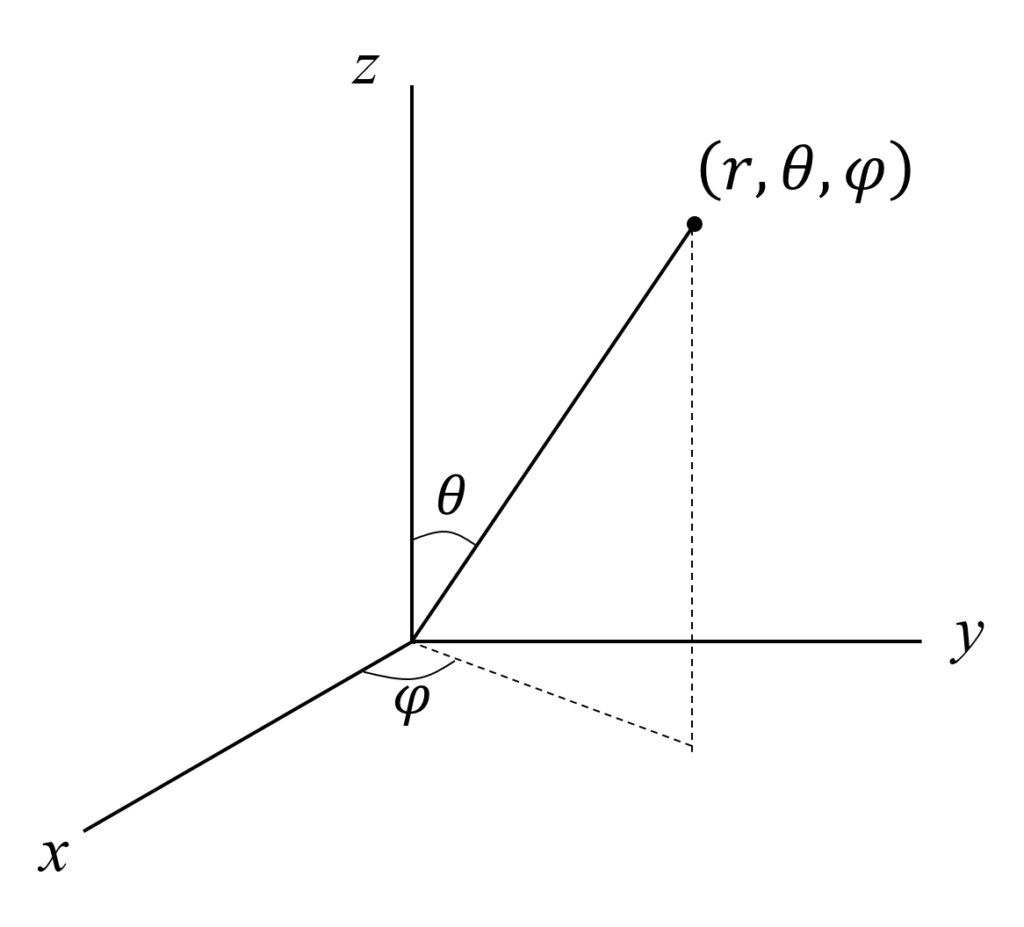
答えは以下の様になります。
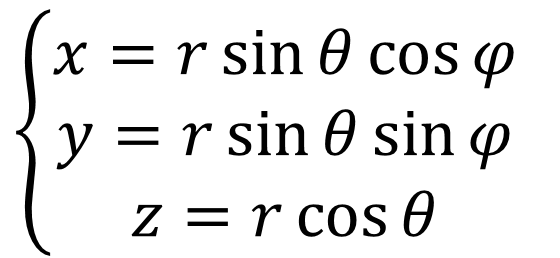
これの導出をやっていきます。
問題のイメージ
3次元における極座標のイメージ

まずは、r, θ, φのイメージから考えていこう。座標ってのはそもそも「位置情報」だよな。
直交座標なのか極座標なのかは、その位置情報の表し方が違うだけなんだ。

rってのは中心からの距離。これはわかりやすいんだけど、θとφがイマイチよく分からないのよね。
高校数学の場合は2次でr, θとx, yの関係が掴みやすいじゃない?
でも角度が2種類出てきたとたん、よく分からない感じになってくる・・・。

角度が二つあるんだよな。その角度がどう変わると、点がどう移動するのかイメージ掴みにくいってことだな?

うん。

じゃあ、3次元極座標を地球に当てはめてみよう。緯度がθ、経度がφに相当する。
ここ東京は北緯35°、東経140°だ。俺の故郷、熊本は北緯32°、東経130°だ。
地球上でφが10°マイナスになるということは、約1000km西へ移動することになる。
じゃあ、問題。北緯43°、東経141°の日本の大都市はどこだ?誰もが知ってるであろう、7大都市の一つだ。

う~ん。8°北へ移動するから・・・800kmくらい・・・?
仙台はもうちょっと近いから・・・札幌?

正解。札幌だ。今、頭の中で地球を思い浮かべただろう?8°北へっていうことはまさしくθが8°変わったことに相当するな。

もう一回上の図を見てみよう。地球における北緯90°、すなわち北極点がθ=0になる。そして、地球上で南へ移動することを思い浮かべながらθがだんだん増えていくことを想像してみよう。θ=90°は地球におけるどこだ?

赤道?

そうそう。さらに南へ移動していく。θがだんだん増えていく。θ=180°が?

南極点ね!

その通り!

じゃ、その次。φ=0°が本初子午線としよう。イギリスのグリニッジ天文台を通る線がφ=0°だ。そして、θ=55°に固定する。北緯35°の位置だな。φが増えていくにつれてヨーロッパからアジアへ。そしてφ=140°の位置の都市は?

東京。

そうだな。そして日本から太平洋へ。φが180°になると?そこは?

日付変更線ね!

そうだな。だんだんわかってきただろ?地球上ではここで西経に切り替わるが、φはこのまま増えていくとしよう。φが増えていくとアメリカの西海岸から東海岸、そしてヨーロッパへ。
最後φ=360°がφ=0°と同じ位置になって地球一周ゴールだ。

なるほど。球ではrが決まれば、球の平面が決まるから、北から南のθと東から西のφの二つを決めれば点になるのね。
直交座標系でzが決まれば平面が決まって、xとyの二つで位置を決定するのと同じなのね。

そうそう。球座標っていうのはそういうイメージだ。
3次元の極座標がイマイチイメージしにくいという方は身の回りにある丸いものを考えて、縦の線と横の線を考えてみましょう。今回は地球を例にとりましたが、スイカ、バスケットボールなどをイメージしてみてもいいかもしれません。スイカを真っ二つに切るという行為は数学的に言えば
φ=0°の位置における断面を取得する。
と表現できます。イメージできましたでしょうか?
求めるべき3つの線
球座標のイメージの話をしたところで、もう一度問題を見てみましょう。とある任意の点(r, θ, φ)は(x, y, z)で表すとどう表現されるか?という問題で、その解答が与えられていて、その導出をする問題でした。
ここで、この問題は
z軸に垂直な線①、x軸に垂直な線②、y軸に垂直な線③を補助線として引いたときに、赤色の線と青色の線と緑色の線の長さを求めよ。
という問題に置き換えて考えることができます。
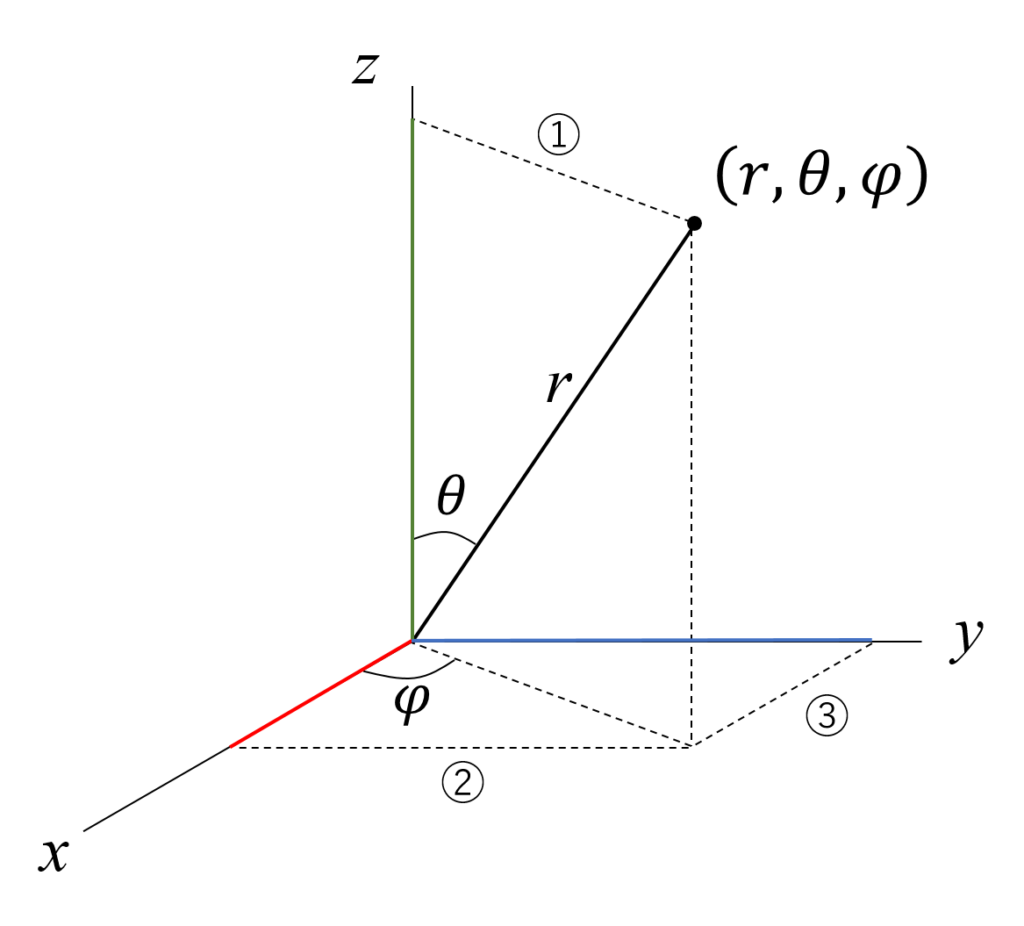

任意の点(r, θ, φ)は(x, y, z)で表すとどうなるか?っていう問題は、その任意の点における(x, y, z)の座標を求めよっていうことになる。
xの座標はすなわち赤色の線の長さだ。

まずは、下の図の紫色の線の長さを求めてみる。
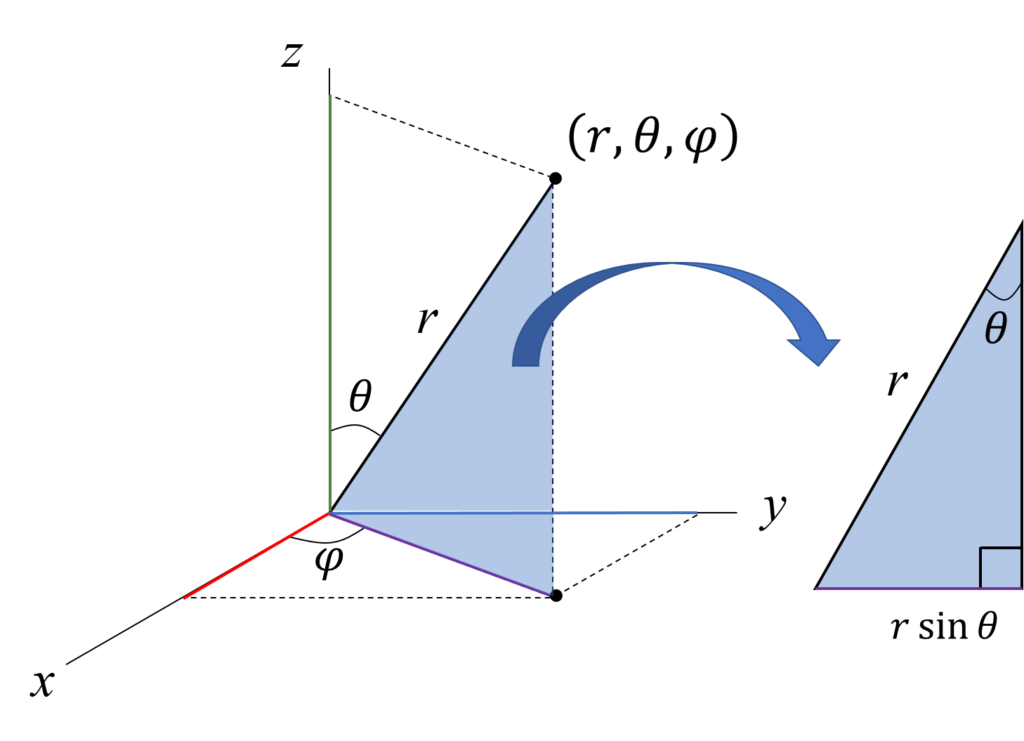

これ、青色の三角形の頂点とθって、対角だから同じ角度になるのね。

そうそう。 そうしたときに、青色の三角形を取り出してみよう。
これでもう、紫色の線の長さが分かるだろ?

rsinθになるのね。三角比だ。懐かしい。

次に、同じようにxy平面上で三角形を取り出してみる。
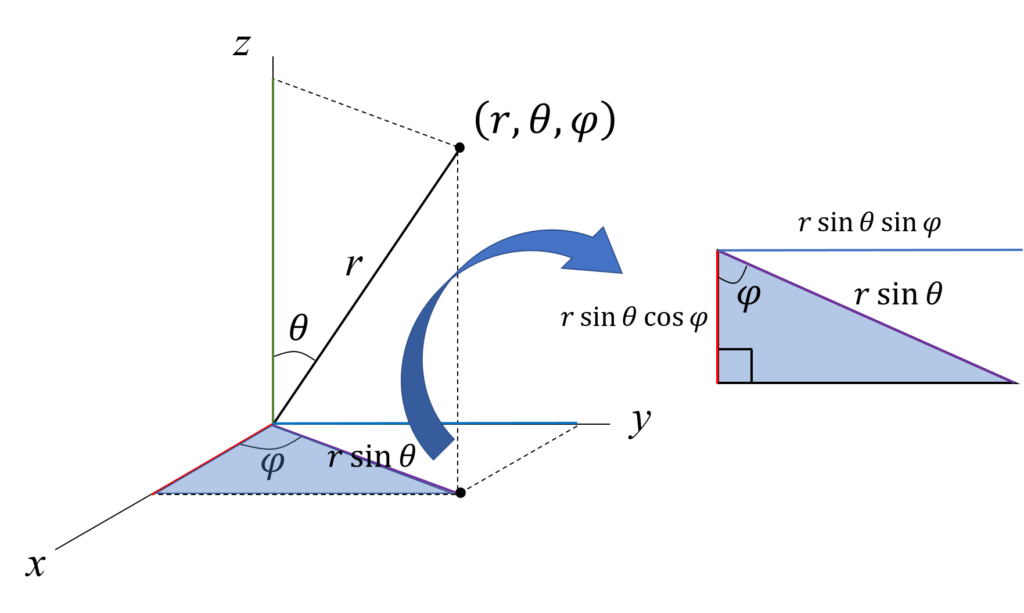

そしたら、赤色の線の長さは、rsinθにコサインがかかってrsinθcosφになるのがわかるか?

うん。そうだね!あと、青色の線はrsinθsinφね!

これ、補助線②とxが垂直ってことに気づかないと、この回答はできないわね。
真上から見たら垂直なんだけど、この図みたいにナナメから見たらわかりづらいよね・・・。

でも、3次元を2次元である紙に表現するには、こうするしかないんだよな。ここがこの問題の難しさだと思う。
3次元のモノを真上から見たら?横から見たら?どうなる?っていう想像がしっかりできないと、理解が難しい。

さて、赤色の線の長さ、すなわちx座標と青色の線の長さ、y座標が分かったところで、
最後にz座標を求めてみる。これは簡単でθだけで表現できる。
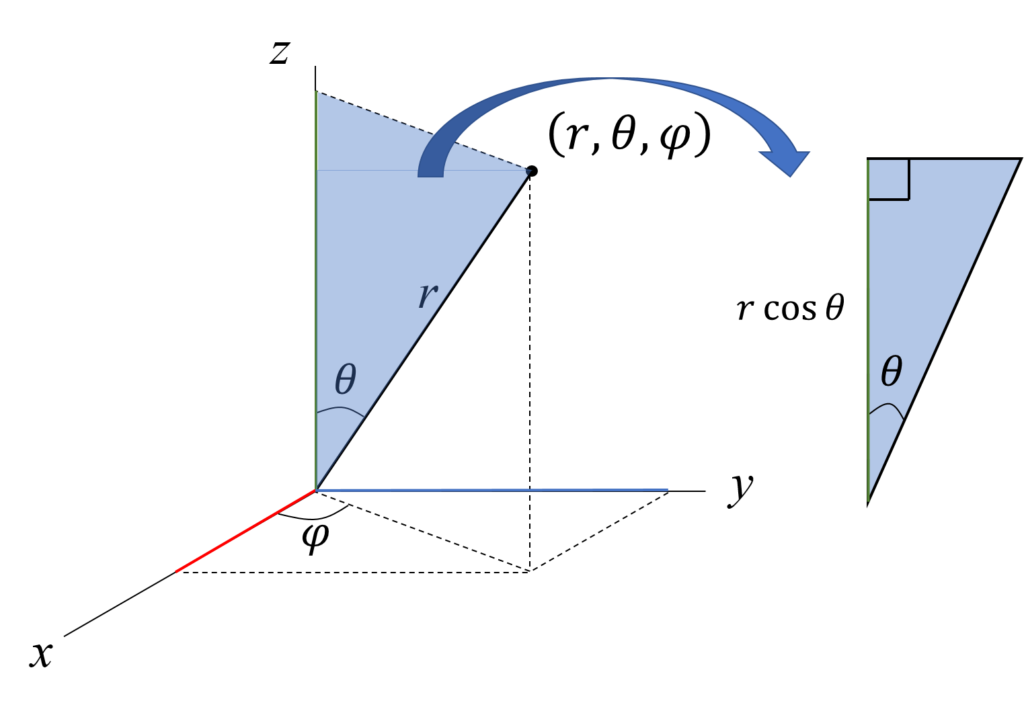

これで、先ほどの関係式が全部揃うよな。
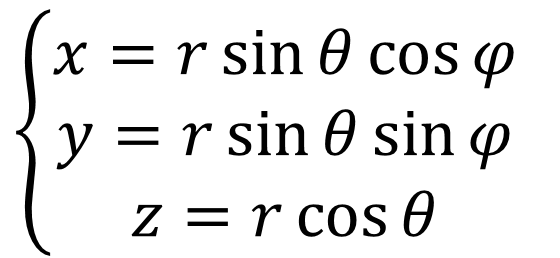

なるほど・・・・。
3次元極座標と直交座標の関係式の公式って、こういう考えで出されるのね~。

・・・ちょっと落ち着いて考えないと混乱するかも。

そうだな。アタマ疲れてボケーッとしているときにいきなりこの問題を出されたらちょっと戸惑うよな。
使っている理論自体はただの数学Ⅰの三角比だけなんだけどさ。
なんつーのかな・・・。空間認識能力?こういうやつが長けてないと今までやった見たみたいに一個一個考えないと混乱しちまう。
俺はあんまり長けてないからな~。こんな風に考えるんだが・・。

ワタシも苦手かも・・・。少なくとも長けてはいないと思うな~。
まとめ
今回は、直交座標と極座標の変換の公式の導出ということで、簡単にできそうで、簡単にできない問題を取り上げてみました。
こういうのがまるで2次元座標を取り扱うようにスパッとできる人がいたら羨ましいですね。
 らい・ぶらり
らい・ぶらり


コメントを残す