資料請求番号:TS36 TS41 TS91

スポンサーリンク
電験や制御工学で登場するラプラス変換を詳しく解説
微分方程式は物体の運動、化学反応、電気回路などあらゆる現象を説明するのに重要な方程式で、世の中の自然現象はほぼすべて微分方程式で表現できるといっても過言ではないでしょう。微分方程式というのは自然現象を操ってモノを作る工学の世界では非常に重要な方程式なのです。
しかしながら、微分方程式を解くのは簡単なことではありません。微分方程式の型に合わせて様々なテクニックを駆使して解きます。その中で複雑な微分積分が多くあります。中には、数学理論で解くことのできない微分方程式も存在します。
そのため、方程式を離散化して代数方程式に落とし込んで解く方法を学び、活用することが多いです。
その一つが↓こちら↓
工学をするにあたっては、微分方程式を数学的に解くよりも、このように
微分方程式を代数方程式、すなわち、「ただの足し算引き算掛け算割り算」にすり替えて解く技術の方が重要視される傾向にあると思います。
ルンゲ・クッタ法あるいはその他の数値計算技術のほかに微分方程式を代数方程式にする方法があります。
それがラプラス変換なのです。
本記事ではラプラス変換の基本的な理論の説明とその演習として、簡単な
回路の解析、物体の運動の解析
をラプラス変換で行います。
注:こちらは、初めて、あるいは久しぶりにラプラス変換に触れる人向けに、詳しく(悪く言えばくどく)解説を行っています。
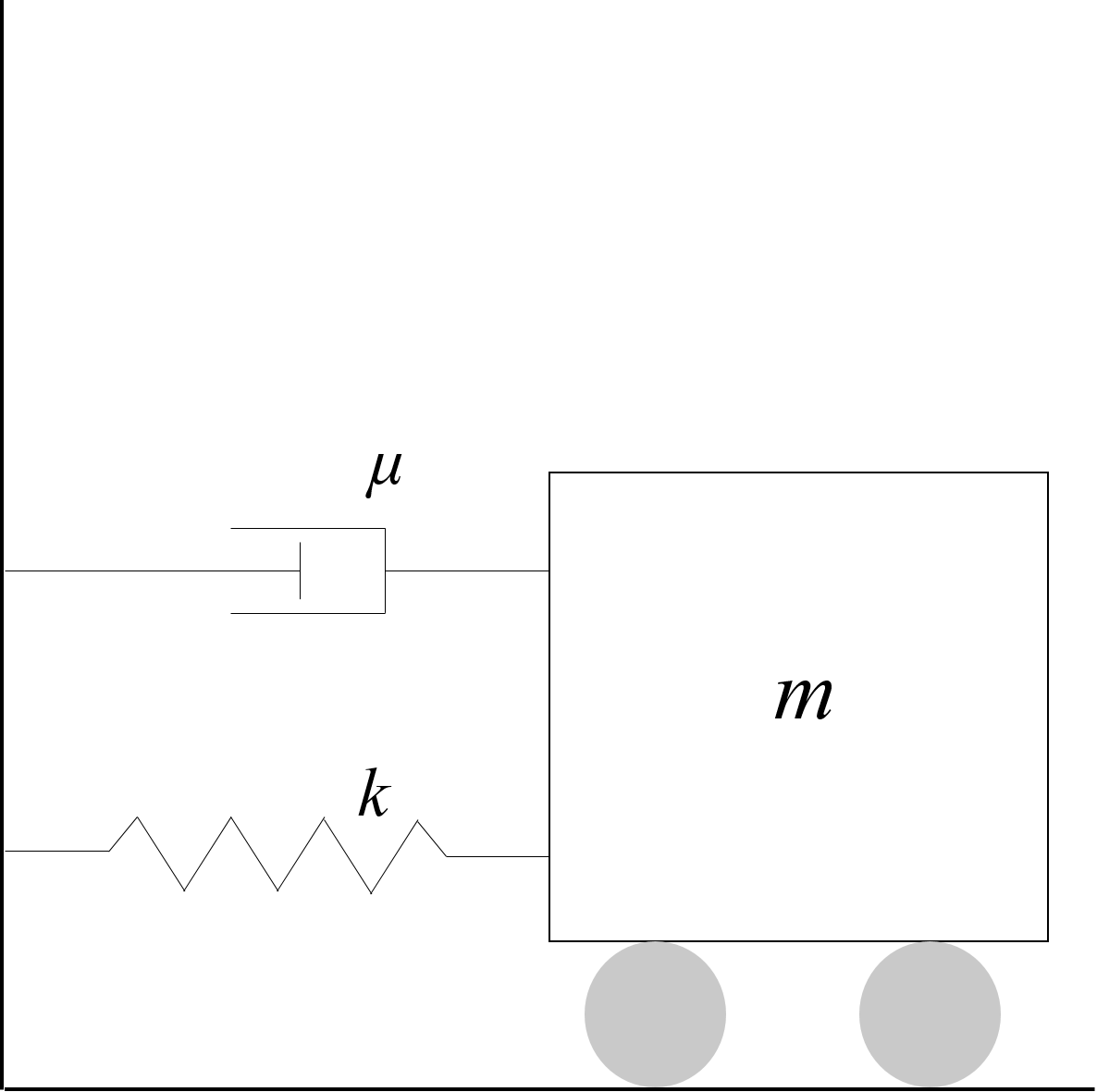
ラプラス変換に慣れている方は↓こちら↓で高度なRLC回路のステップ応答問題や機械力学のバネーダッシュポット系のインパルス応答問題に挑戦してみるといいと思います。
ラプラス変換は電験3種で登場する
 ファビー
ファビーなぁ、ストーク。ラプラス変換、教えてや~・・。
 ストーク
ストークなして、そげなことば聞くん?職場で知識求められよるん?
 ファビー
ファビーう~んと・・・。
 ファビー
ファビー課長から「電験3種取ってくれると嬉しいなぁ~・・・。」言われて。
 ストーク
ストーク電験!?オマエ、QC(※)やろ?
 ファビー
ファビーせやねん。せやねんけど、QCの仕事には割と慣れてきたけん、そっちの方もやらせたいと思われとるんちゃうやろか?
(※QC=Quality Control=品質管理)
 ストーク
ストークあ~・・・。仕事に余裕のある風な感じを出しちゃったんやろな~。
 ファビー
ファビーせやねん。やってしもた~思てな。
 ストーク
ストークハハッ・・・。
 ファビー
ファビーで、電験3種の本ば見よったら、ラプラス変換いうものがあって・・・。
 ストーク
ストークあ、なるほど、そういうことな。
 ファビー
ファビーなんか、ラプラス変換問題は捨てよっても合格点ばとれよるけん、勉強しなくても大丈夫いう話があるんやけど・・・。
 ストーク
ストークう~ん。俺はそういうの好いとうないけん、ばってん、そういう考え方もあってもええんとちゃう?
 ファビー
ファビーアタシも最初そう思うとったけど、ちゃんと理解したら点取り問題になると思うけん、それに身近にすうがくのメチャクチャ詳しいストークがおるわけやから、ええ機会かな~思て。
 ストーク
ストーク俺はそんなに詳しかないけどな。ただ、ラプラス変換みたいな基礎的な話ならできるたい。
 ファビー
ファビーラプラス変換を基本いうてる時点でアタシからしたらだいぶ詳しいと思うけん、教えてや~!!
 ストーク
ストークわかったわかった。
ラプラス変換の表記
 ストーク
ストークラプラス変換言うのは、ただ単に積分の計算ばしよって、関数の形を変えるだけのことなんやが、
教科書参考書の種類や先生教授の好き勝手で色んな形の表記があることが、多くの人のラプラスアレルギーを発症させとる原因やないかと思うたい。
 ファビー
ファビー・・・表記?
 ストーク
ストークこんなんとか
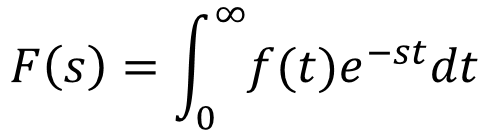
 ストーク
ストークこんなん。
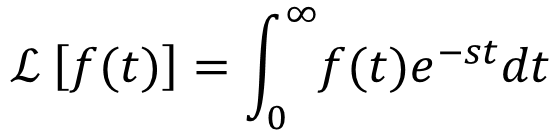
 ファビー
ファビーせやねん!こんな感じのちょっとオシャレな感じのLの意味が全く分からんくてなぁ~・・・
 ストーク
ストークわかるなぁ~・・・。いきなりこんな感じのわけわからん記号使わんといてや~思うよなぁ~。
 ファビー
ファビーうん・・・・
 ストーク
ストークちゃんと教科書読めば説明ばしよるんやが、その説明がまた・・・
 ファビー
ファビーややこしか~・・・。
 ストーク
ストークせやな。まぁ、1つ目の式と2つ目の式はやっていることとしては同じたい。右辺が全く同じやろ?
 ファビー
ファビーうん。
 ストーク
ストークある関数f(t)いうものがあって、そのラプラス変換というものはF(s)やℒ[f(t)]と表記する。そして、その定義は
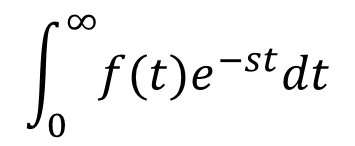
 ストーク
ストークであるいうこと。
 ファビー
ファビー・・・・。
 ストーク
ストークわかったような、わかんないような・・・って感じやろ?
 ファビー
ファビーせやな。
 ストーク
ストークじゃ、簡単な例題を通してラプラス変換いうものを”感じる”いうか・・・こんな感じなのか~みたいなのを掴んでみような。
ラプラス変換を初めて学ぶ際、一番最初に困るのが、突然わけわかんない記号を使われることではないでしょうか?F(s)やℒ[f(t)]のような記号は、定義を理解し、計算に慣れた人にとっては非常に便利なのですが、その慣れた感覚で初学者に説明してしまうと疑問だらけになってしまいます。そういう意味で
f(t)のラプラス変換について
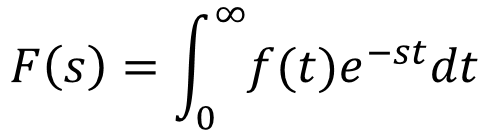
と
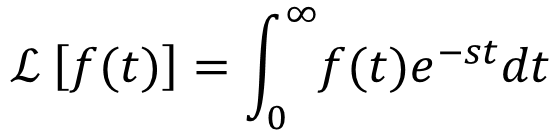
の二通りの表記の方法があるということをまず、頭の中に入れておいていただきたいのです。
これを了承して計算問題を何度も解いていくと、だんだんラプラス変換を使った微分方程式の解法に慣れてくることができます。
数学は頭でっかちな学問に見えて割と「勘」というのが必要な学問でして、その勘と言うのは繰り返しの演習で獲得することができます。
ラプラス変換をとりあえずやってみる
f(t) = 1とf(t) = t のラプラス変換
 ストーク
ストーク数学でもな、つべこべ言わず、とりあえず言われたとおりにやってみようという考え方が必要でな、せやからとりあえず、ラプラス変換の計算をやってみよう言うことでな。
 ファビー
ファビーそうなんか・・・・。
 ストーク
ストーク算数の勉強はまず「1+1=2」から始まるやろ?
なして「1+1=2」なんか考えるよりも、「1+1=2」なんだということを覚えよったら次に進めるやろ?それと一緒たい。
 ファビー
ファビーふぅ~ん。
 ストーク
ストークというわけでな、とりあえず、まずはf(t) = 1のラプラス変換を求めてみような。
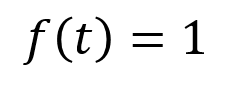
 ストーク
ストーク関数f(t)のラプラス変換いうものは
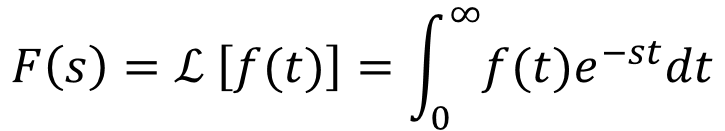
 ストーク
ストークなわけたい。ここで、何を計算すればええかわかるか?
 ファビー
ファビーえっと・・・f(t)を1とすればええと?
 ストーク
ストークせや。
 ファビー
ファビーほんなら・・・・
 ファビー
ファビーこうか?
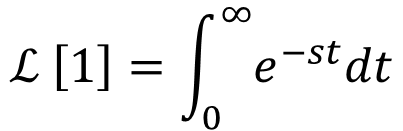
 ストーク
ストークおっ、ええ感じたい。
 ファビー
ファビーe・・・
 ストーク
ストークeの微積分って、これでやったやん。覚えとるか?
 ファビー
ファビーあ~・・・微積分してもそのままなヤツ・・・?
 ストーク
ストークせや。せやけど、e-stを微分ばすると-se-stになるたい。合成関数の微分やな。
 ファビー
ファビー-stだけ微分して前に出すヤツやな。
 ストーク
ストークせやな。それで、今回は積分したいけん、微分ばするとe-stになるような関数が答えやから・・・
 ファビー
ファビー・・・こんなんでどんな?
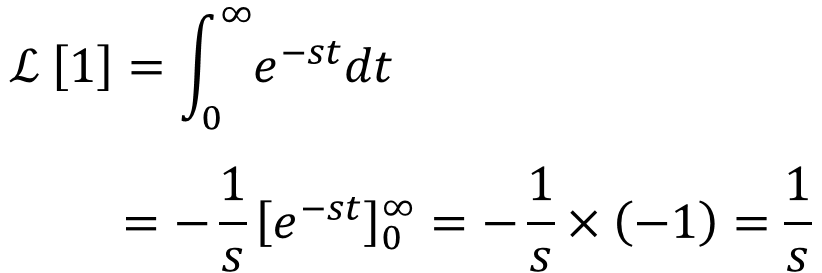
 ストーク
ストークおっけーおっけー。e-stのsについて、無限の極限をとるとゼロになることとか、0乗は1いうこともちゃんと覚えよったようやな。
 ファビー
ファビーえへへ~
 ストーク
ストーク(むぞらし~なぁ~)
 ストーク
ストークじゃあ、それと同じ感じで今度はf(t) = tをラプラス変換してみる。
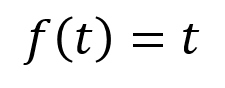
 ファビー
ファビーそしたらこの積分をすればええと?
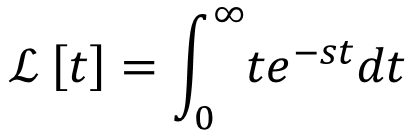
 ストーク
ストークせやな。
 ファビー
ファビーあ~これ、部分積分の問題や・・・。
 ストーク
ストークこれ見て思い出しながらゆっくりやってみいや。
 ファビー
ファビーえっと・・・。
 ファビー
ファビーこう?
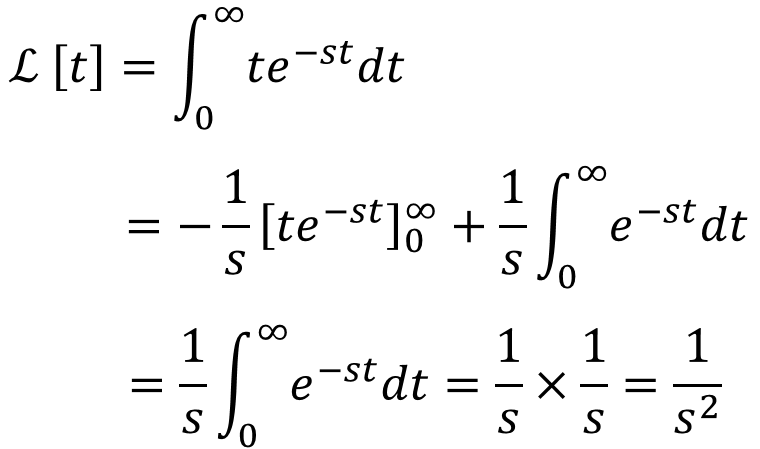
 ストーク
ストークええよ!正解!
 ファビー
ファビーやった!
ラプラス変換をやってみてわかること
 ストーク
ストーク今、f(t) = 1とf(t) = tのラプラス変換をやってみたやろ?
 ファビー
ファビーうん。
 ストーク
ストークまとめるとこんな感じやんな。
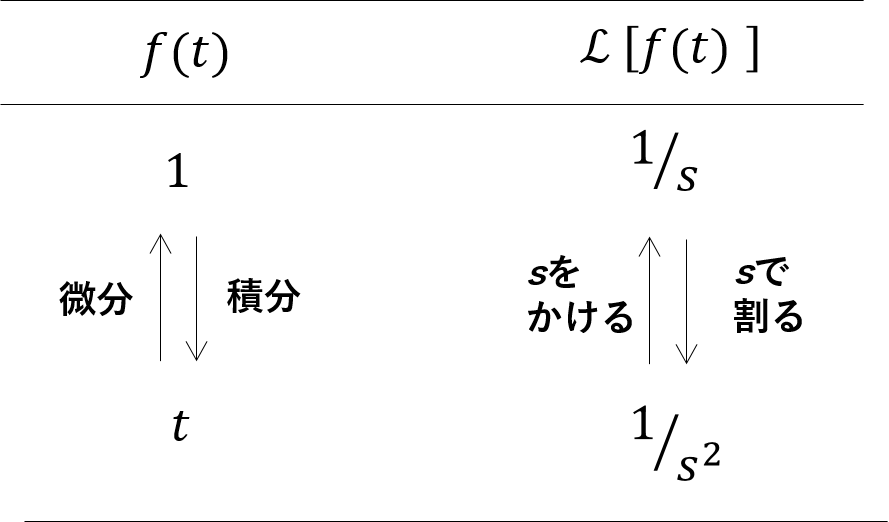
 ストーク
ストーク元の関数f(t)では微分と積分の関係やったものが、ラプラス変換しよった後の関数ℒ[f(t)]やったら掛け算と割り算の関係になった。と言えるたい。
こうやって、微分積分の計算は難しいけん、せやったら、四則演算できるようにしたらどんな?
って考え方がラプラス変換たい。
 ファビー
ファビーあ~・・。e-stって、微積分したらsが出たり引っ込んだりするだけで関数の形ば変えんと、そういうeの性質をうまいこと使って微分積分を掛け算割り算にしてしまうんや~。かしこか~。
 ストーク
ストークせやろ?そういう一種のアハ体験みたいなものが面白いたい、数学は。数学っつーか、自然科学はな。
いろいろなラプラス変換
ラプラス変換表
 ストーク
ストーク電験3種の本とか解説見たときにラプラス変換表みたいなのなかった?
 ファビー
ファビーあったよ。意味わからんかったけど。
 ストーク
ストーク今のオマエならわかると思うたい。もう一回みてみな?
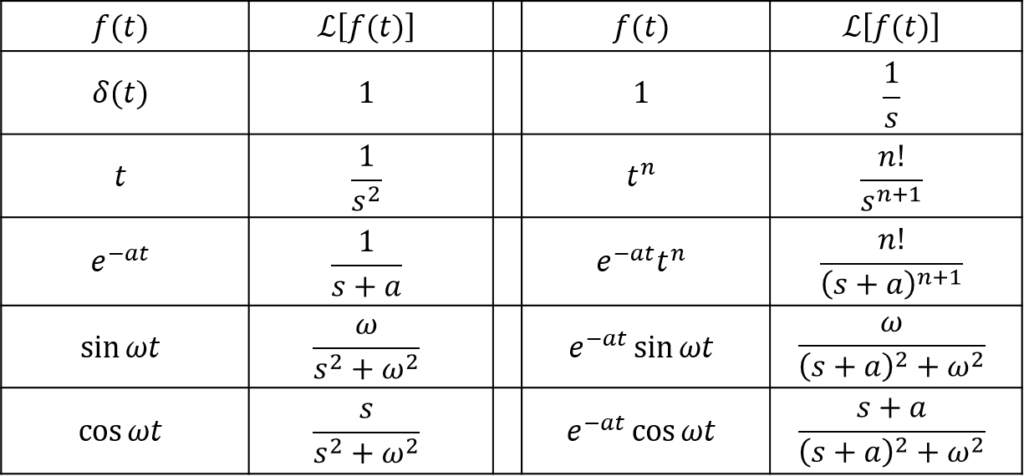
出典:斎藤制海・徐 粒 共著,計測と制御シリーズ 制御工学 -フィートバック制御の考え方ー,第1版第1刷,2003年,pp.19
 ファビー
ファビーあ~。アタシが1とかtとかで計算したことと、おんなしことをsinωtとかcosωtとかにやれば、こんな風になるけん、使ってな~っていうのがこの変換表なんか~。
 ストーク
ストークせや。せやからぶっちゃけな、ラプラス変換表とラプラス変換による解答の手順さえ身に着けてしまえば、数Ⅲでやるようなクソ難しい微積分ばせんでも微分方程式が解けるということたい。
 ファビー
ファビーせやったら、しっかりマニュアル化しさえすれば、四則演算さえできれば誰でも微分方程式を解けるということになって、回路の設計とかができるようになると。
 ストーク
ストークそういう意味でもな、学歴不問な電験3種の試験に堂々とラプラス変換いうものがあると思うたい。
 ファビー
ファビーえ?資格試験受けるのに学歴ば必要なんかあるん?
 ストーク
ストークたくさんあるたい。例えば俺らで身近なモノでいえば危険物甲種。これはたしか化学関係の大卒以上か、化学に関係する単位を15とるか、数年の実務経験があるかが受験資格やったと思うたい。
 ファビー
ファビーそうなんや~。大学ば行くか、実務積むかいずれにせよ何年か化学に触れとらんと受けさせてもらえんのや~。
ラプラス変換を使えば何階微分でも代数方程式にできる
 ストーク
ストークそれで、ラプラス変換で微分方程式を解くにあたって知っておきたい性質いうか、公式がこれ。
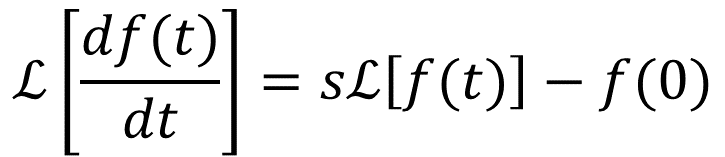
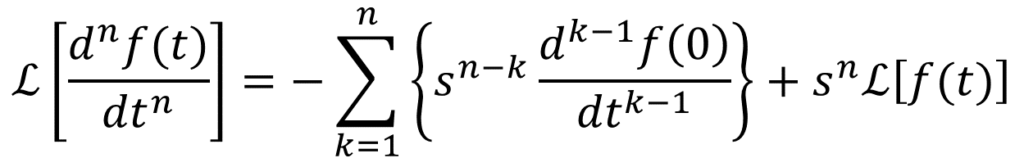
 ファビー
ファビー無理。特に2つ目。
 ストーク
ストークまぁまぁ、そんな最初から投げ出さんといてや。とりあえず1つ目だけ理解しような。
 ストーク
ストークdf(t)/dtてのはf(t)の一階微分やな。それでそのラプラス変換いうものは、微分する前の関数f(t)だけで表現できる!ってのがこの公式。
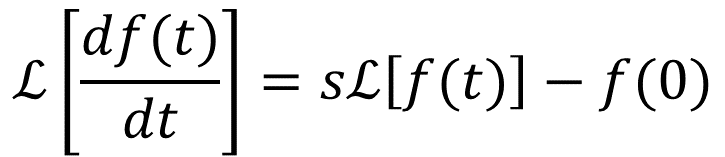
 ファビー
ファビーえっと、これ、上にちょんちょんがいくつついとっても、ちょんちょんがない式に変換できるということ?
 ストーク
ストークうえにちょんちょん?
 ストーク
ストークあ~。f’とかy’のこと?
せやねん。f’はdf/dtでy’はdy/dtな。例えばy” + 3y’ + 2y = 0を解けいう微分方程式の問題があったとしても、この公式ば使えばちょんちょんをなかったことにできるたい。
 ファビー
ファビーどれだけ微分しとっても、元の関数f(t)のラプラス変換さえできとったら微分方程式解けるんか~。便利やけんね~。
 ストーク
ストークせやねん。じゃあ試しにな
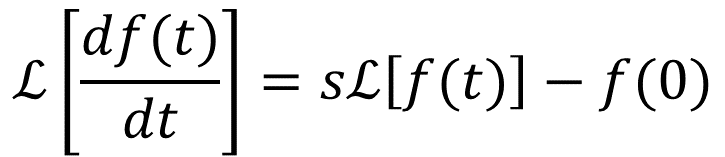
 ストーク
ストークを証明してみると、こんな感じになる。
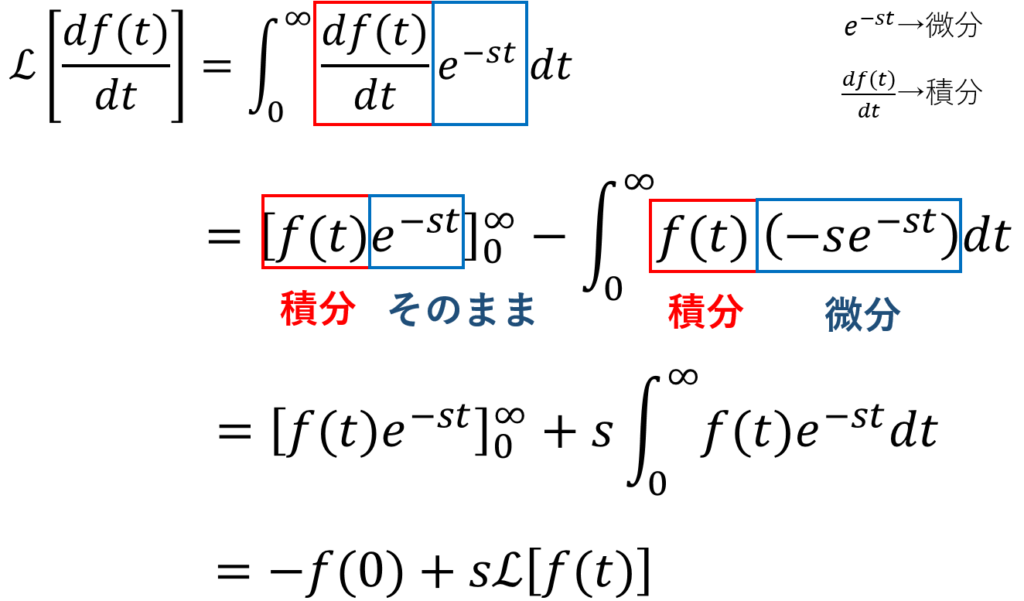
 ファビー
ファビーあ~ここでも部分積分の知識ば使っとると。部分積分大事なんやな~。
 ストーク
ストークせやで~大事やで~。大事やから理系の大学の入試では部分積分の問題は頻出やけん。部分積分の問題に慣れとらんヤツがラプラス変換とかしだすと落単しよるからな。
 ファビー
ファビーらくたん?
 ストーク
ストーク単位を落とすいうことたい。ロクに勉強もせんと、カネだけ積んで大学入りよると不幸になるで~・・・。
 ファビー
ファビー(そうなんか~・・・。)
 ストーク
ストークそれで、これを一般化して何階微分でも使えるようにした公式がこれたい。
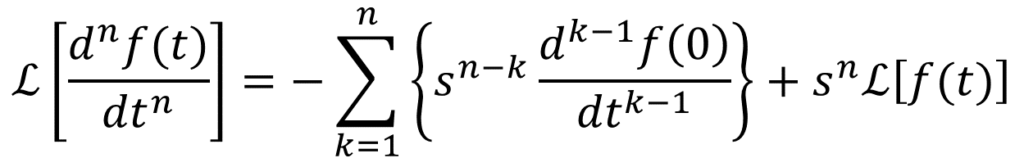
 ファビー
ファビーこれとか特に無理そうや。
 ストーク
ストークまぁ、一個一個式変形を追ってな、じっくり考えたら、
あ、こんなもんか。ってなると思うたい。とりあえず、導出だけ示しておくな。
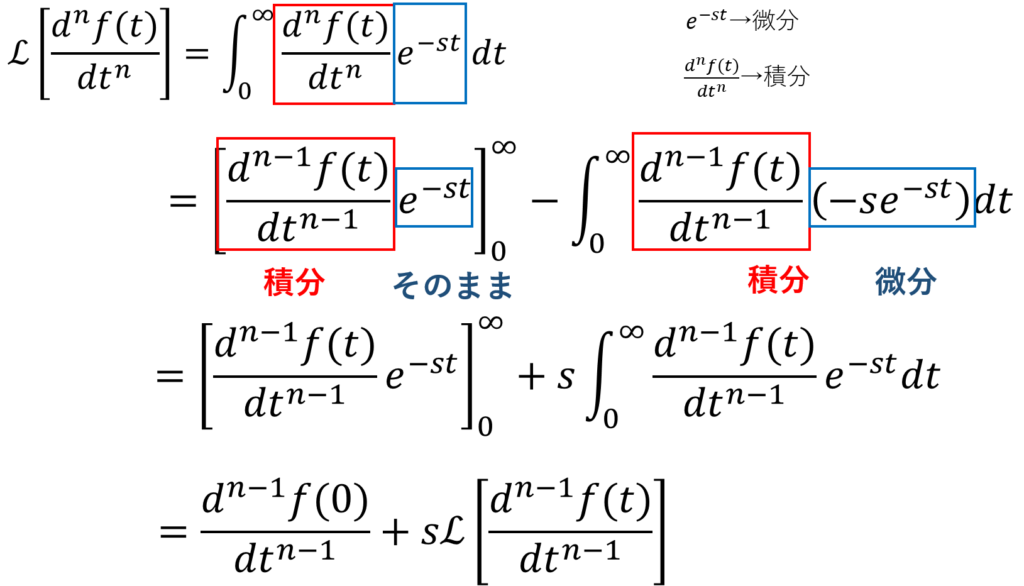
・・・①
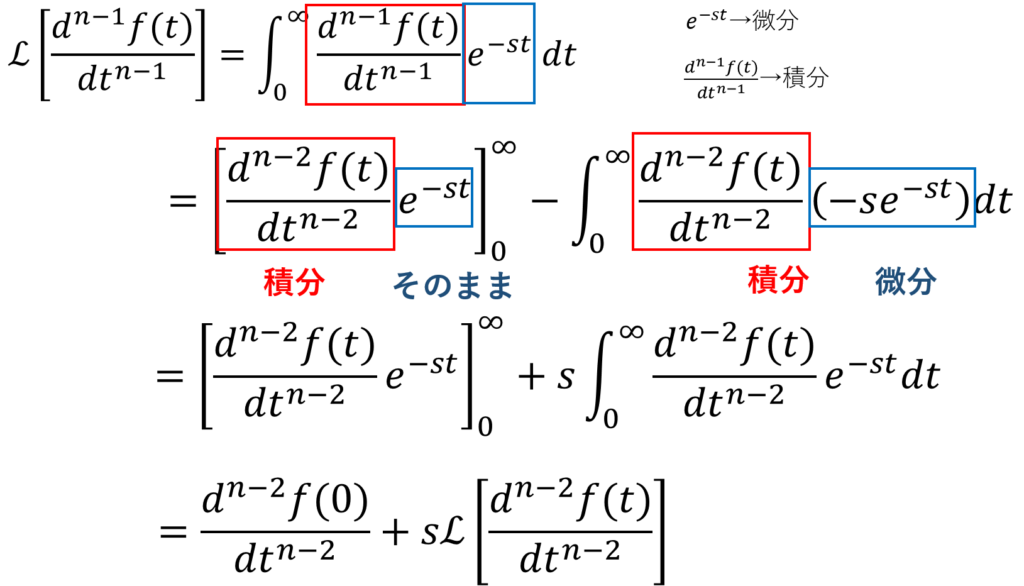
・・・②
①、②より

ラプラス変換を使って微分方程式を解く
RL直列回路
各項をラプラス変換する
 ストーク
ストークじゃあ、実際にラプラス変換使って微分方程式を解いてみるたい。
 ファビー
ファビーえ~・・・。もうやるの・・・?
 ストーク
ストーク言うたやろ?実践あるのみやって。まずは、こんな簡単な回路の方程式からやってみたらどんな?

 ファビー
ファビーあ、これは抵抗とインダクタンスを直列につないだ時の方程式や。

 ストーク
ストークおっ、よう勉強しとるな。「抵抗RとインダクタンスLの直列回路にt=0で直流電圧Vを印加したときに回路に流れる電流i(t)を求めよ。」と言う問題でな、この微分方程式ば解けば電流値iが求められるたい。
 ストーク
ストークまず、それぞれの項をラプラス変換するたい。
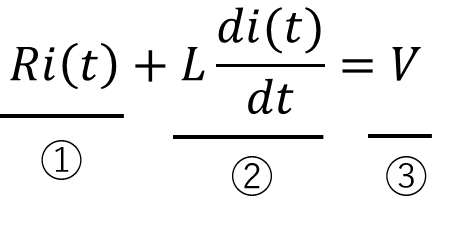
 ファビー
ファビーえっと~・・・。Rは定数で、i(t)をラプラス変換せないかんから・・・
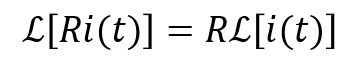
 ファビー
ファビーあれ?i(t)のラプラス変換???
 ストーク
ストークわからんやろ?わからんに決まっとるたい。i(t)の関数の形が求めるべき答えなんやから。
 ファビー
ファビーえ~これじゃあ先に進めないよ~!
 ストーク
ストークとりあえず、i(t)のラプラス変換の形として
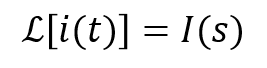
 ストーク
ストークと、置いてみてはどんな?
 ファビー
ファビーなしてI(s)?
 ストーク
ストークラプラス変換を大文字で表現しとくという風習があるのと、ラプラス変換することによってtの関数はsの関数にすり替わるたい。さっきy(t)=1とy(t) = tで計算したやろ?
 ファビー
ファビーそっか~。そういやそうやったな~。
 ストーク
ストークそしたら、1項目はこれでよか。
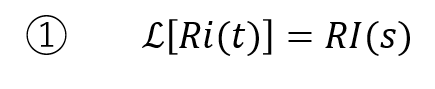
 ファビー
ファビーほう・・・意外とあっさり・・・。
 ストーク
ストーク2項目は1階微分が入っとるけん、さっきの公式
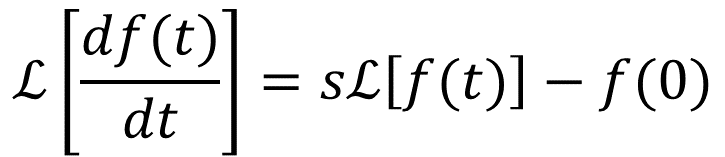
 ストーク
ストークをつかって変換してみな。
 ファビー
ファビーえっと・・・
 ファビー
ファビーこうか?
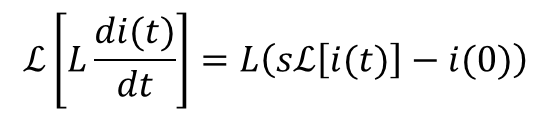
 ストーク
ストークせやな。t=0で電圧かけとるわけやから、t=0の瞬間では電流が一切流れとらんことはわかるな?
 ファビー
ファビーうん。
 ストーク
ストークということは?
 ファビー
ファビーこうか?
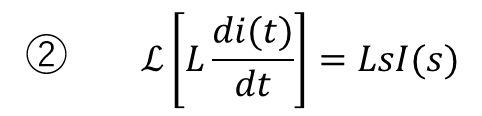
 ストーク
ストークええよ。その調子!
 ファビー
ファビー最後のVはV×1と考えて・・・こうやな。
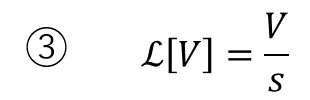
ラプラス変換してできた代数方程式を計算する
 ファビー
ファビーこれで、こういう方程式ができると。
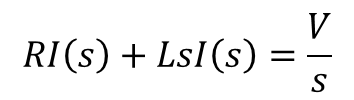
 ストーク
ストークああ、こういう、微分のない、ただの足し算引き算割り算掛け算、つまり四則演算しかない方程式を代数方程式というたい。これをI(s)=ナントカの形にする。これやったら、誰でもできるやろ?
 ファビー
ファビーせやな。こうやろ?
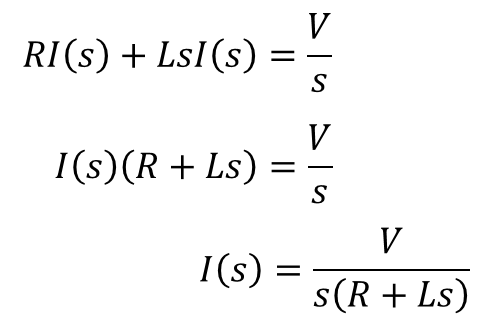
 ストーク
ストークせやせや。それで右辺をラプラス逆変換すればええ。
 ファビー
ファビーぎゃくへんかん?
 ストーク
ストークラプラス変換されたsの方程式を元の時間の方程式に戻すんや。
 ファビー
ファビーえ~・・・またなんか難しい微分積分ばせんといかんの・・・・?
 ストーク
ストークいやいや、代数方程式を解いてできた関数とラプラス変換表にある関数に当てはめていくだけたい。
ラプラス逆変換で元の関数に戻して解を得る

出典:斎藤制海・徐 粒 共著,計測と制御シリーズ 制御工学 -フィートバック制御の考え方ー,第1版第1刷,2003年,pp.19
 ストーク
ストークこれがラプラス変換表やったな。
 ファビー
ファビー同じような形が見当たらんのやけど。
 ストーク
ストークじゃあ、こんな風にしてはどんな?

 ファビー
ファビーあ~こないな感じやったら、1/sとか、1/(s+a)とかが当てはまりそうやけん・・・A,Bってなんなん?
 ストーク
ストークとりあえず、置いてみた定数。この定数を求めて、s(R+Ls)のような形の分母の分数をからsとR+Lsをそれぞれ分母とする二つの分数に分ける数学的操作を部分分数分解というたい。
 ファビー
ファビーぶぶぶぶぶ・・・。
 ファビー
ファビーぷ…….。iiii
 ストーク
ストークぶぶんぶんすうぶんかい。な。こっちで詳しい説明ばしとるから、ここではサクサクいくで。
 ストーク
ストークまず、V/s(R+Ls)を、sとR+Lsを分母とする二つの分数に分けるとき、両辺にsを掛けてから、s=0を代入しよったら、Aだけ残る。こうしてAが求められる。
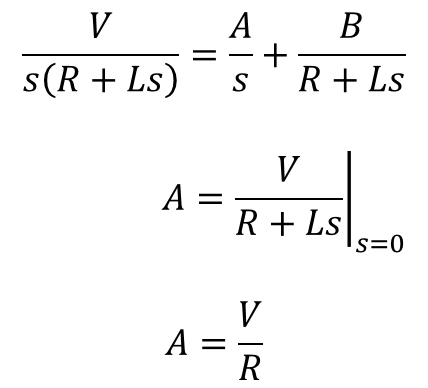
 ストーク
ストーク同様に両辺にR+Lsをかけて、s=-R/Lを代入しよったらBだけ残って、Bも求められる。
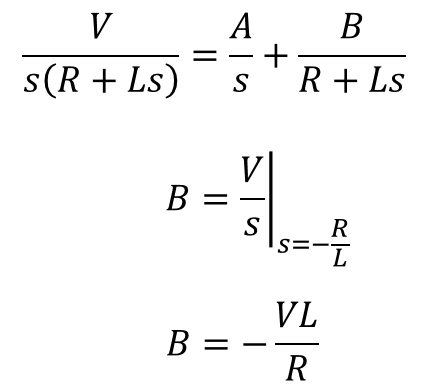
 ストーク
ストークこうして、V/s(R+Ls)は以下のように部分分数分解される。
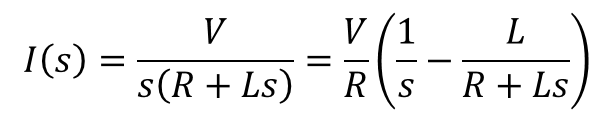
 ファビー
ファビーほう~・・・。
 ストーク
ストークまぁ、これもたくさん演習問題やれば慣れてくるけん、ラプラス逆変換したいときに部分分数分解が必要になることは多いから、たくさん演習してな。
 ファビー
ファビーはぁ~い(*´Д`)。学問に王道なしやなぁ~。
 ストーク
ストークそれはアリストテレスの言葉でな、ええ言葉やと思うが、その約2000年後に発明されたこのラプラス変換が王道みたいなもんやけん。ラプラス変換表使えば、誰でも簡単に微分方程式ば解けちまう魔法の方法やけん、パラドクスみたいやな。
 ファビー
ファビーふぅ~ん・・・。
 ストーク
ストークで、この方程式をラプラス逆変換する。
 ファビー
ファビーあ!これ逆変換しよったら、I(s)はi(t)になって、答えばわかると?
 ストーク
ストークせやせや!そういう仕組みたい!
 ファビー
ファビーなるほど~
 ストーク
ストークな、おもろいやろ?ラプラス変換表から、この二つの式が出てくるたい。
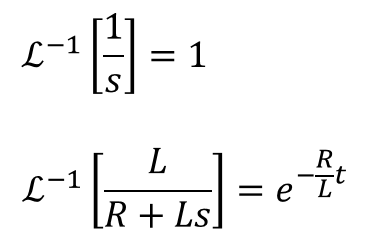
 ファビー
ファビー-1ってのは・・・あ、ラプラス変換表を左から右に見たときはℒで右から左に見たときはℒ-1なんやな。
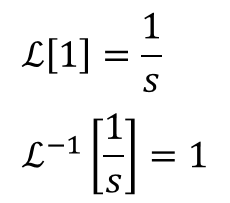
 ストーク
ストークせやせや。そしたら、もう答えは目の前やけん。どんな感じばなる?
 ファビー
ファビーこうやろ?
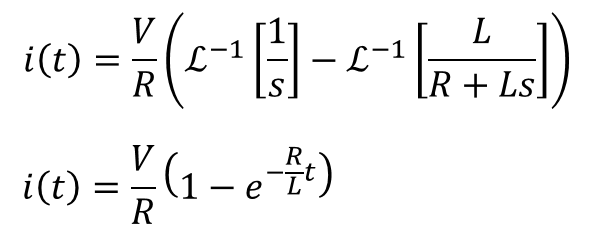
 ストーク
ストークおっけ~正解!おめでとさん!
 ファビー
ファビーやった!
物体の運動方程式
各項をラプラス変換する
 ストーク
ストークじゃあ、次の問題な。
 ファビー
ファビーえ~・・・。またやるの・・・?
 ストーク
ストーク言うたやろ?数学はたくさん演習したら身につくて。今度はこれ

 ストーク
ストーク高さy0から静かに物体を落としました。t秒後における物体の位置y(t)を求めなさい。という問題たい。
 ファビー
ファビーふぅ~ん。とりあえず、それぞれの項をラプラス変換したらええんやろ?

 ファビー
ファビーえっと~・・・。この2階の微分言うものはさっきの公式
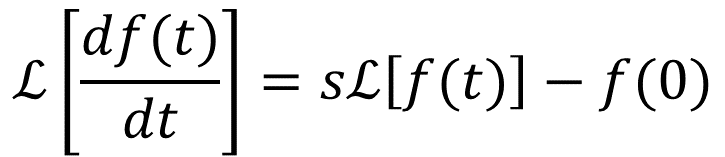
 ファビー
ファビーを2回使えばよか?
 ストーク
ストークせやな。
 ファビー
ファビーそしたらこんな感じになると?
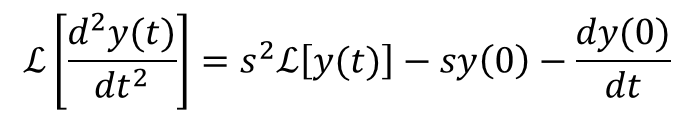
 ストーク
ストークええ感じええ感じ。そして「高さy0から静かに物体を落としました。」ということはy(0) = y0やろ?それに、「静かに物体を落としました」と言うことはdy(0)/dt = 0になるたい。このイメージはつくか?
 ファビー
ファビー静かに物体ば落としたいうことはその時の速度がない。と言うことはyの1階微分がゼロ言うことやろ?
 ストーク
ストークせやせや。そしたらこんな感じに書き換えられるな。
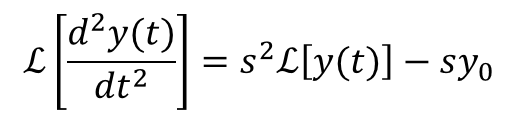
 ファビー
ファビーy(t)が求めるべき関数で、これの正体がまだわからんけん、とりあえず、Y(s)と置いておくんやな。
 ストーク
ストークせやな。
 ファビー
ファビーそしたら、①のラプラス変換は、こうなるけんね。
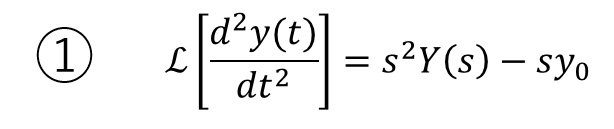
 ストーク
ストークああ、ええ調子たいね。
 ファビー
ファビーそれで、②のラプラス変換は、-gっていう重力加速度の定数しかあらへんのやけど、これを-g×1と考えてラプラス変換ばするけん、こんな感じ?

 ストーク
ストークせやせや。ええのー。感覚ばついて来とるたいね。
 ファビー
ファビーえへへ~・・。
 ストーク
ストーク(やっぱり、むぞらしかね~・・・。)
ラプラス変換してできた代数方程式を計算する
 ファビー
ファビーそしたら、こういう方程式ができあがって、Y(s)について解けばええけんね。
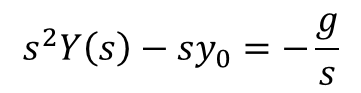
・・・・
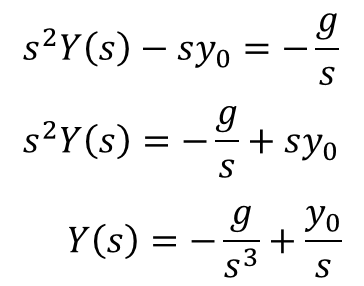
 ファビー
ファビーできた~!
 ストーク
ストークお~っ!感覚が掴めてきたようやな~。じゃあ、次、ラプラス逆変換たい。
ラプラス逆変換で元の関数に戻して解を得る

出典:斎藤制海・徐 粒 共著,計測と制御シリーズ 制御工学 -フィートバック制御の考え方ー,第1版第1刷,2003年,pp.19
 ストーク
ストーク例えば、ラプラス変換表によるとtnのラプラス変換はこんな感じ
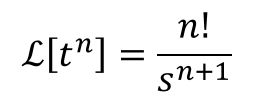
 ストーク
ストークそうしたときに、-g/s3を逆ラプラス変換したいなら、n=2を代入すれば、こんな情報ば得られる
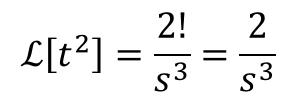
 ストーク
ストークと、いうことは、2/s3の逆ラプラス変換、これをℒ-1で表すと、こうなる。
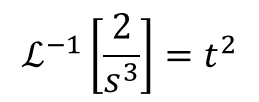
 ストーク
ストークせやったら、-g/s3の逆ラプラス変換は-1/2 gt2になることがわかるたいね。
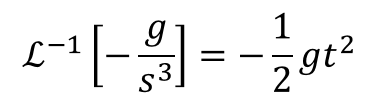
 ファビー
ファビーおお~っ、すごか~。でもこれ、ラプラス変換表のどの情報ば使うんかの判断は割と慣れが必要な部分がありそうやけんな。
 ストーク
ストークせやな。せやから、どんどん演習問題をやるのがええたいね。
 ファビー
ファビーそっか~。結局泥臭いんやな。
 ストーク
ストークせやで~。あと。y0/sやけど、これはすぐに逆変換できるな。
 ファビー
ファビー1/sの逆ラプラス変換やから結局1になって、y0しか残らんとね。
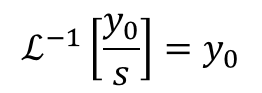
 ストーク
ストークそしたら、この微分方程式の答えいうのはこんな感じになるな。
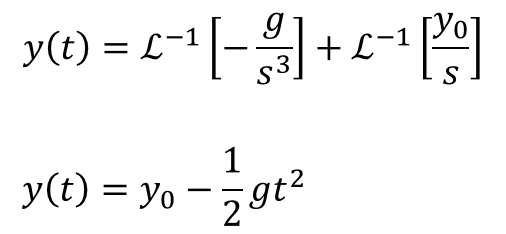
 ファビー
ファビーあ~・・・アタシが最終的に答えば出したかったのに・・・。
 ストーク
ストークああ、すまねぇ。
まとめ
今回は、微分方程式を解く方法の一つとしてラプラス変換を紹介し、簡単な微分方程式をラプラス変換で解きました。電験三種に出てくるように回路設計はもちろん、制御理論を考える上でもラプラス変換は非常に重要です。プロセス制御においてはプロセスの因と果が微分方程式で結ばれていることが多く、そこをラプラス変換によって代数方程式によって入力と出力の関係を比で表すということが行われています。
ラプラス変換による微分方程式の求解に慣れてきたら、より高度なRLC回路の問題や機械力学のバネーダッシュポット系のインパルス応答問題に挑戦してみるといいと思います。




















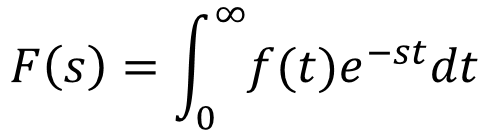

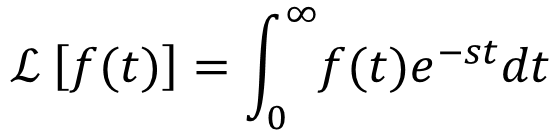








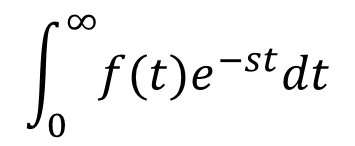





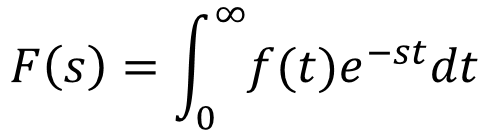
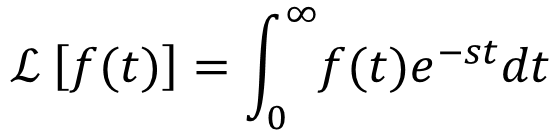





![]()

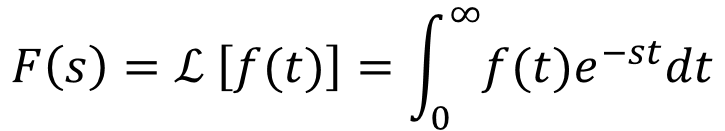





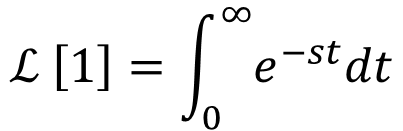








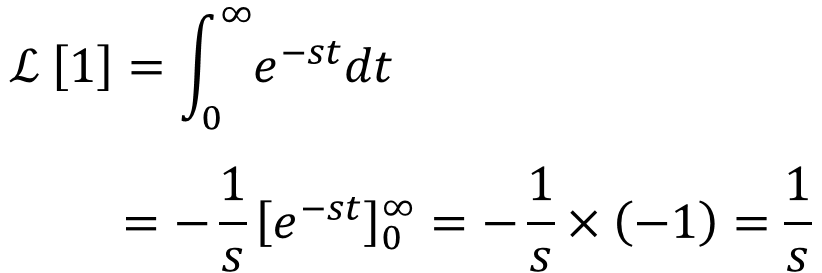




![]()

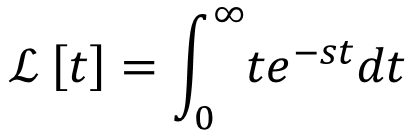





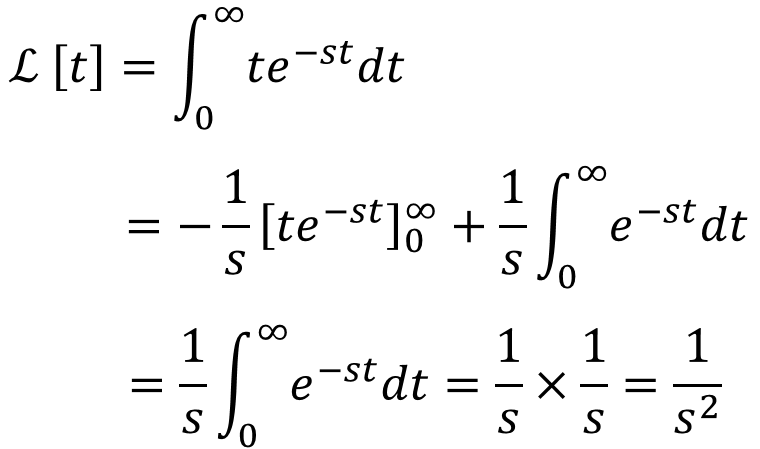





















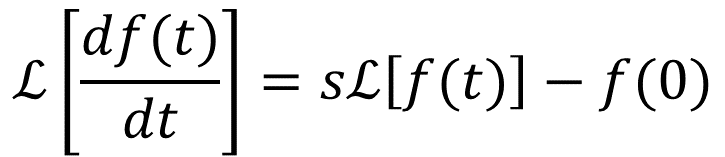
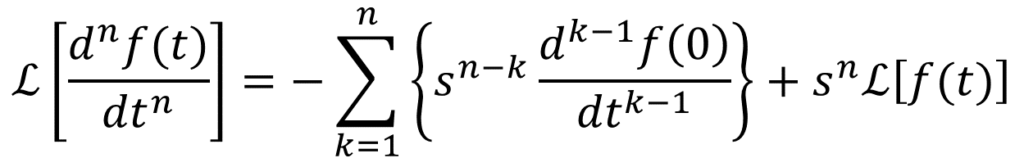



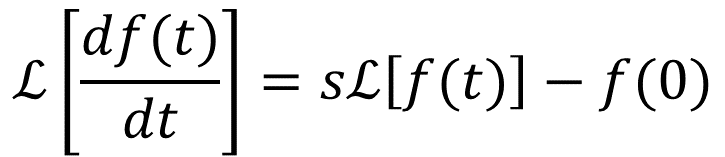





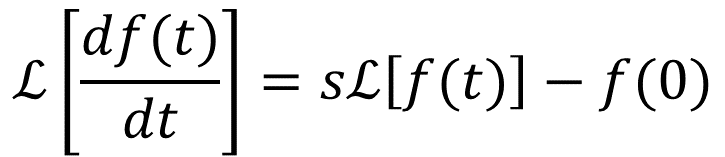








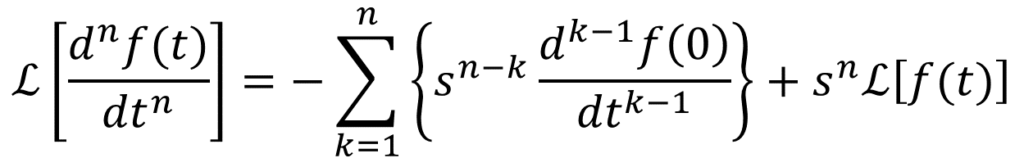













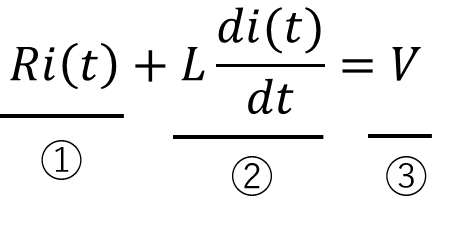

![]()




![]()





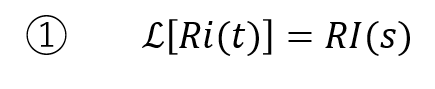


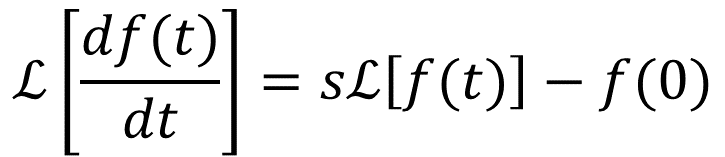







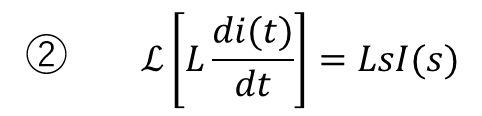


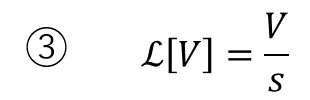

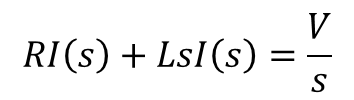


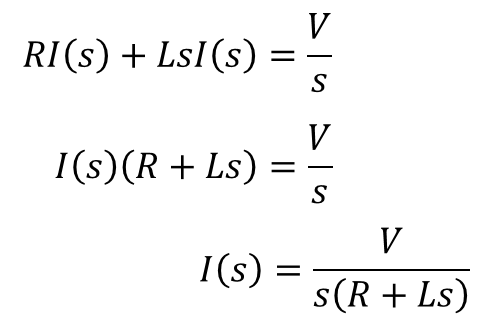
















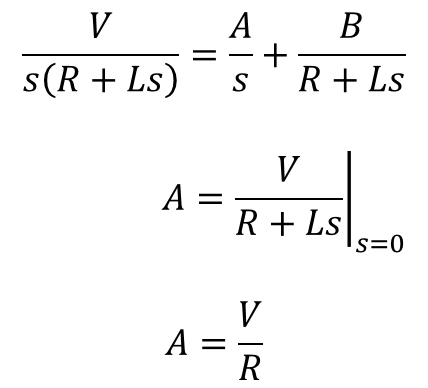

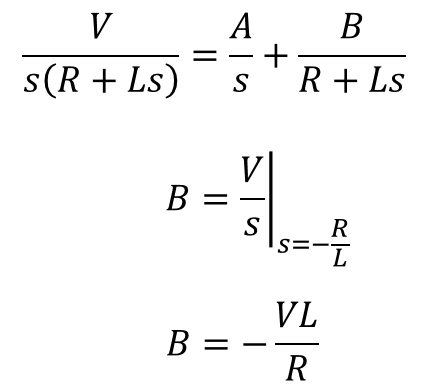

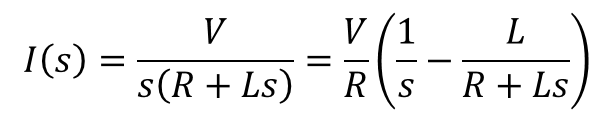










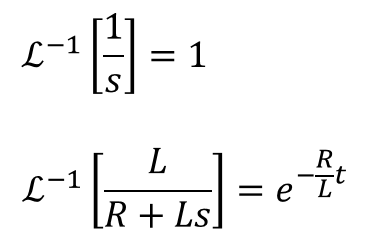



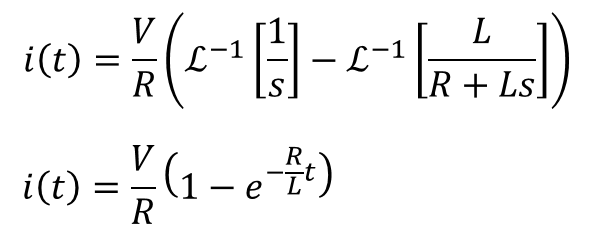










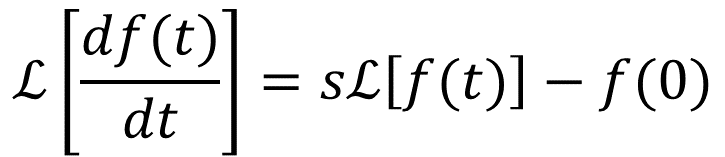



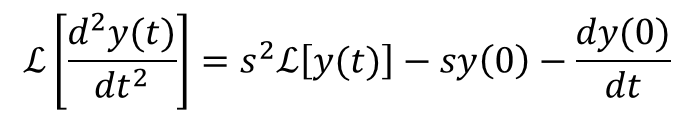



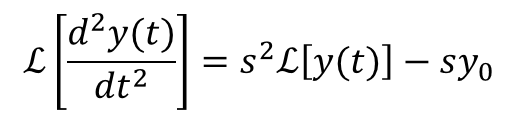

![]()


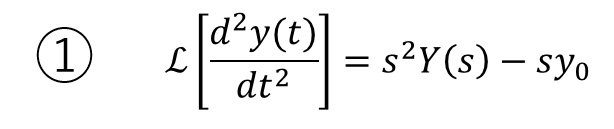







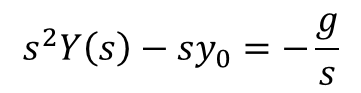
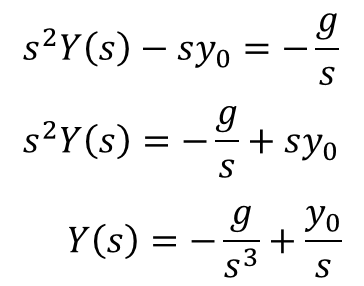




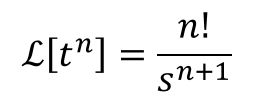

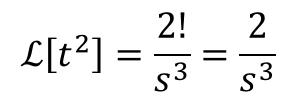

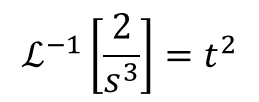

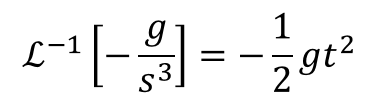





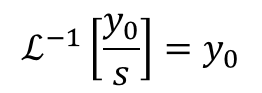

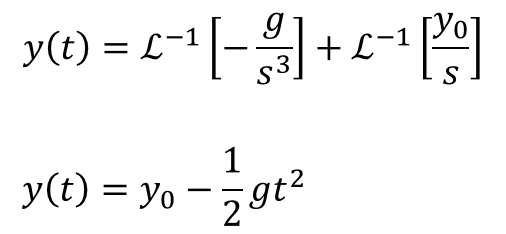


 らい・ぶらり
らい・ぶらり


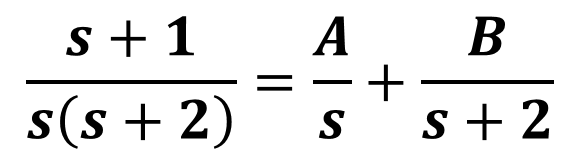


コメントを残す