資料請求番号:TS11
スポンサーリンク部分積分をマスターして国公立大学の入試問題を解いてみよう
高校数学で微積分を学んでいると、部分積分というものに出会うことがあるかと思います。
この部分積分の公式、使うのにはちょっとしたコツが要ります。
今回は、そのコツと部分積分を応用した国公立大学の入試問題を解説したいと思います。
※今回取り扱う部分積分は基礎的内容です。既に
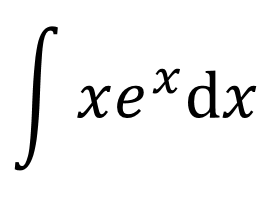
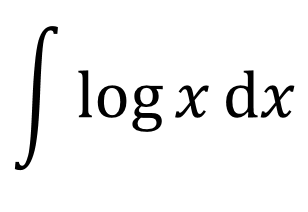
のような積分の計算がスラスラできるような方には易しすぎる内容になると思いますので、ご了承ください。
応用問題はこちら
[blogcard url=”http://shimaphoto03.com/science/pi-irrational/”]
部分積分とは?
二つの微分可能な関数f(x)、g(x)が存在する時、次の公式が成り立つ。
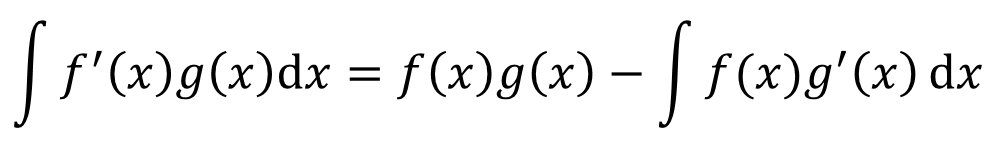

なんかもうね、この公式の時点で意味が分からないねん。積分の中に微分があって、??って感じ。

なるほどな。ファビーさ、例えばf'(x)からf(x)になるときってどんなことをしている?

どんなこと??

あぁ、じゃあ、質問を変えてだな、f(x)からf'(x)を求めるには微分をするよな。じゃあ、
f'(x)からf(x)を求めるにはどうすればいい?

微分の反対やから・・・積分する?

その通りだ。じゃ、もう一回この公式を見てみよう。
f'(x)からf(x)は積分している。g(x)からg'(x)は微分しているんだな。そして、右辺第一項には数学的処理を加えない「そのまま」のヤツもある。


この公式を見ながら、
積分・そのまま・マイナス・積分・微分と10回唱えてみろ。

積分・そのまま・マイナス・積分・微分、積分・そのまま・マイナス・積分・微分、積分・そのまま・マイナス・積分・微分
積分・そのまま・マイナス・積分・微分、積分・そのまま・マイナス・積分・微分、積分・そのまま・マイナス・積分・微分
積分・そのまま・マイナス・積分・微分、積分・そのまま・マイナス・積分・微分、積分・そのまま・マイナス・積分・微分
積分・そのまま・マイナス・積分・微分!!
部分積分のコツ
よくある間違い

ハイ。それじゃあ、この問題を解いてみよう。
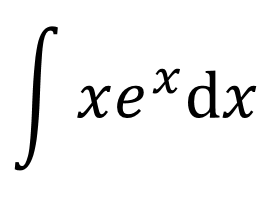

えっと・・・積分・そのまま・マイナス・積分・微分・・・。
・・・・

できないよぉ!!

見してみ。
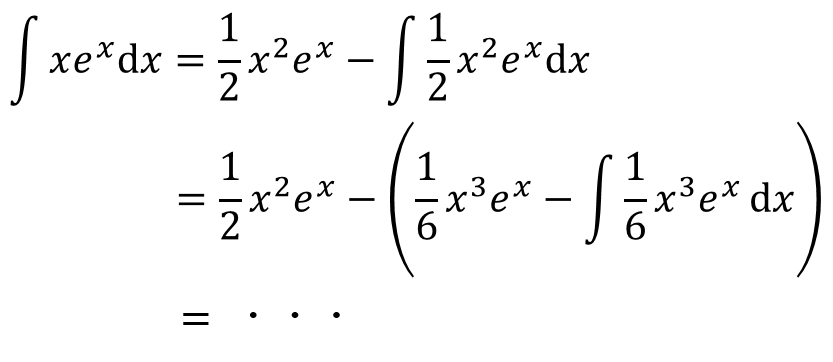

あぁ~。。。これじゃあ、できないんだよなぁ~。。
微分役と積分役

もう!積分・そのまま・マイナス・積分・微分って覚えたのにできないじゃん!

もう一回、この公式を見てみよう。


f(x)は積分されるだけ、g(x)は微分されるだけ、ということに注目だ。

xは積分するとどんどん次数が増えていくやろ?そしたら収拾つかなくなるたい。
俺らのゴールはなるべく簡単な形にすることだ。
だから、xとexがあったときに、どっちを微分してどっちを積分したら簡単になるのか?を考えなくちゃいかんたい。

あ~。。。xを微分すれば1になるからxをg(x)に当てはめて、exをf(x)に当てはめればよかったってこと?

そういうこと!それでもう一回解いてみな。
・・・・

できた!
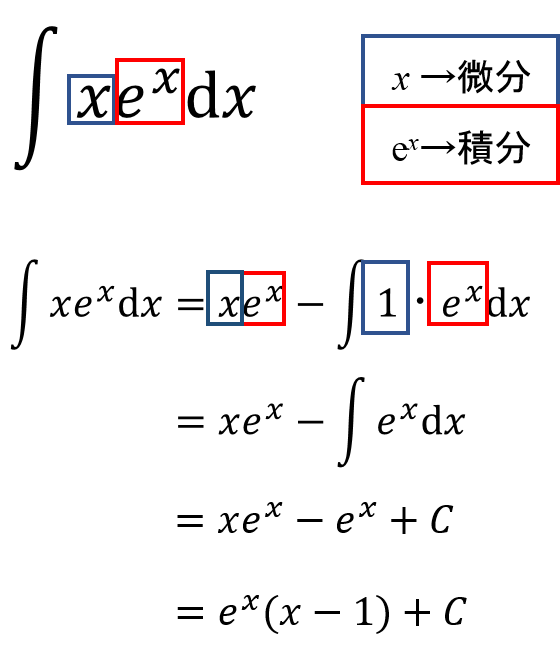

そうそう!こうやって、どっちの関数を微分するのか、どっちの関数を積分するのかをメモっておくとやりやすいよな。
この場合、xを微分役、exを積分役にしてやればいいんだよな。

関数にもな、人間と同じように性格があるったい。
微分すりゃおとなしくなるヤツ、微分しようが積分しようが微動だにしない落ち着いたヤツ、二重人格で微分したり積分すると表裏がひっくり返るヤツ・・・
その性格に応じた役割を与えなきゃいけん。役割論理ってやつですなwwww
数学に慣れるとこういった関数の性格が分かってくるから、xは微分以外ありえないwwwってなるたい。

ふぅ~ん・・・。

じゃあ、次の問題。これは?
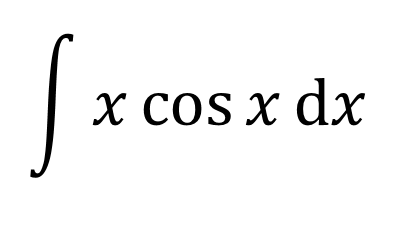
・・・

・・・こう?


そうだな!xを微分役にしてやればいいんだよな。
国公立大学の入試問題を解く

じゃあ、この部分積分を応用した国公立大学の入試問題をやってみよう。

え~、いやいや、ムリやて~!!

大丈夫だ。国公立大学の入試問題といえど、教科書に出てるレベルの問題だ。
出典: 信州大学入試過去問題

信州大学?長野? 長野いいとこやね~!ハイキングにスキー!今はスキーの季節やけんね!

てかもう、nとかやめて~!!ムリや~!!

まぁ、一見難しそうな問題でもな、一個一個考えていきゃ、別にそんなに大したことないから。
そうだな・・・最初。最初の式変形だけ受験テクニックっぽいのがいるたいね。最初の式変形はこうする。
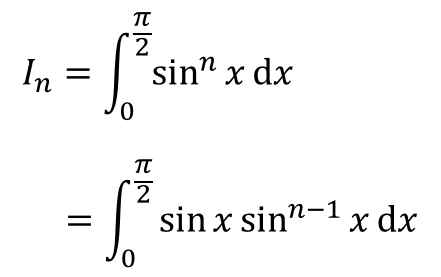

・・・・。

それで、ファビーだったらどっちを微分役にして、どっちを積分役にする?

・・・sinのn-1乗の方を微分して、sinxを積分する。

どうしてだ?

だって、n-1乗を積分するとか難しそうやけん。あと、n-1乗を微分すれば、n-2が出てくるやろ?それって、In-2のもとになったりするん?

そうそう!そういう考え方が大事ったい!
続き、やってみな。
・・・・

・・・・。

・・・・。

・・・・。

・・・・。

(・・・・時間かかるなぁ)。

ああ、やっぱムリや!

どこがムリ?
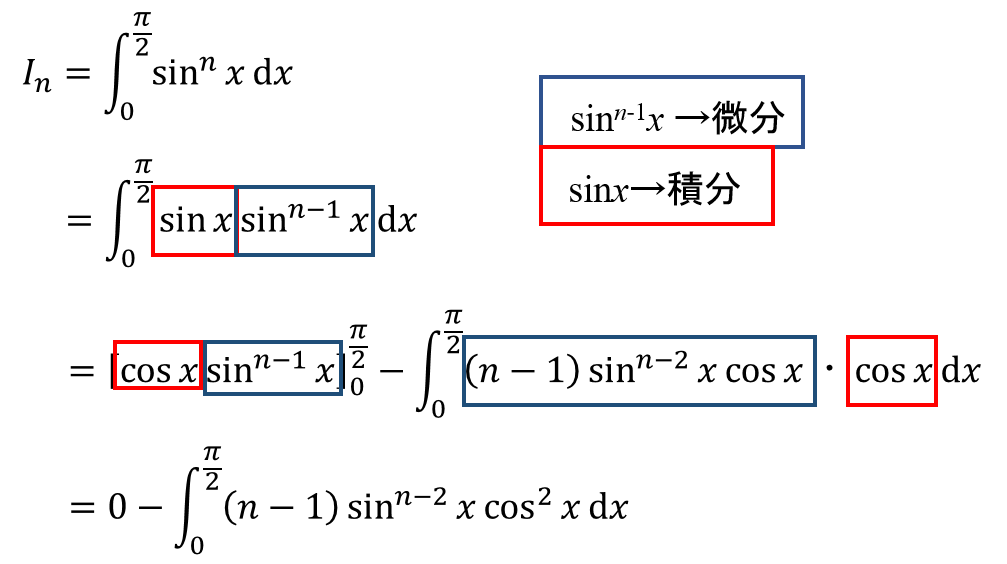

cosの2乗!

あぁ・・・。でも、合成関数の微分が出来たのは良かったな!よくできた!
cosの2乗はな・・・これ。
![]()

あ~、こんな公式、あったなぁ~。

(しょっちゅう使うんだが・・・まぁ、いいか。)
これ使って、続きをやってごらん?
・・・・

・・・・。

・・・・。

・・・・。

・・・・。

(・・・・やっぱり時間かかるなぁ)。

できた!!
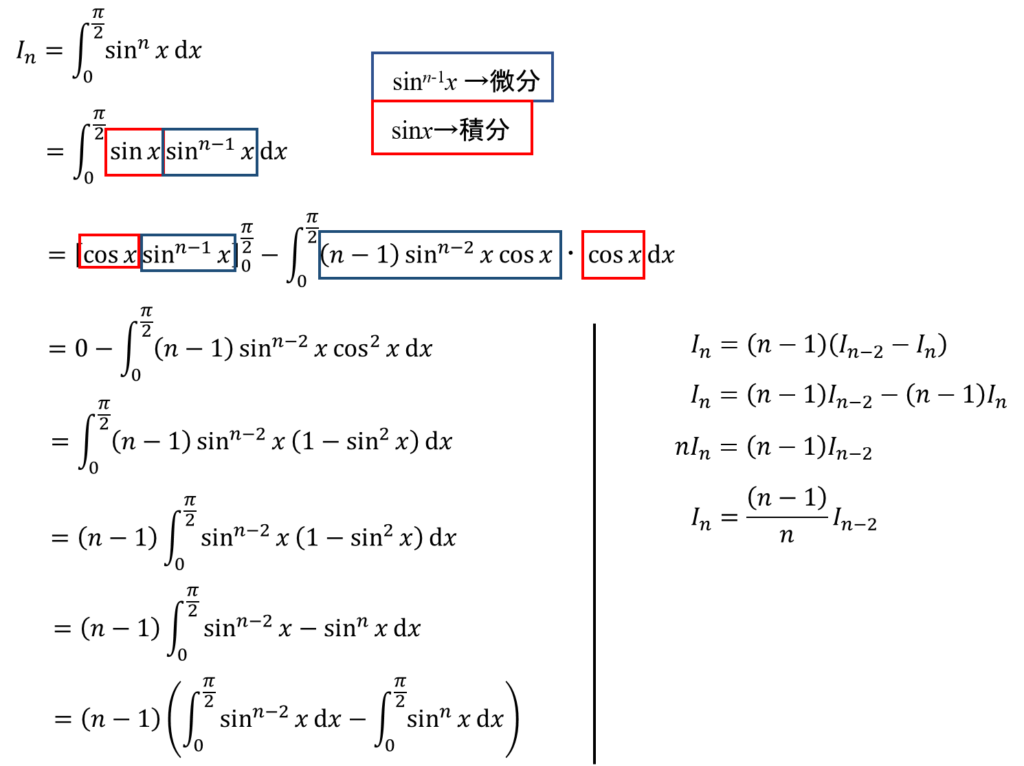

よしっ!じゃあ、(2)もやってみよう。
・・・・・

・・・これでよか?
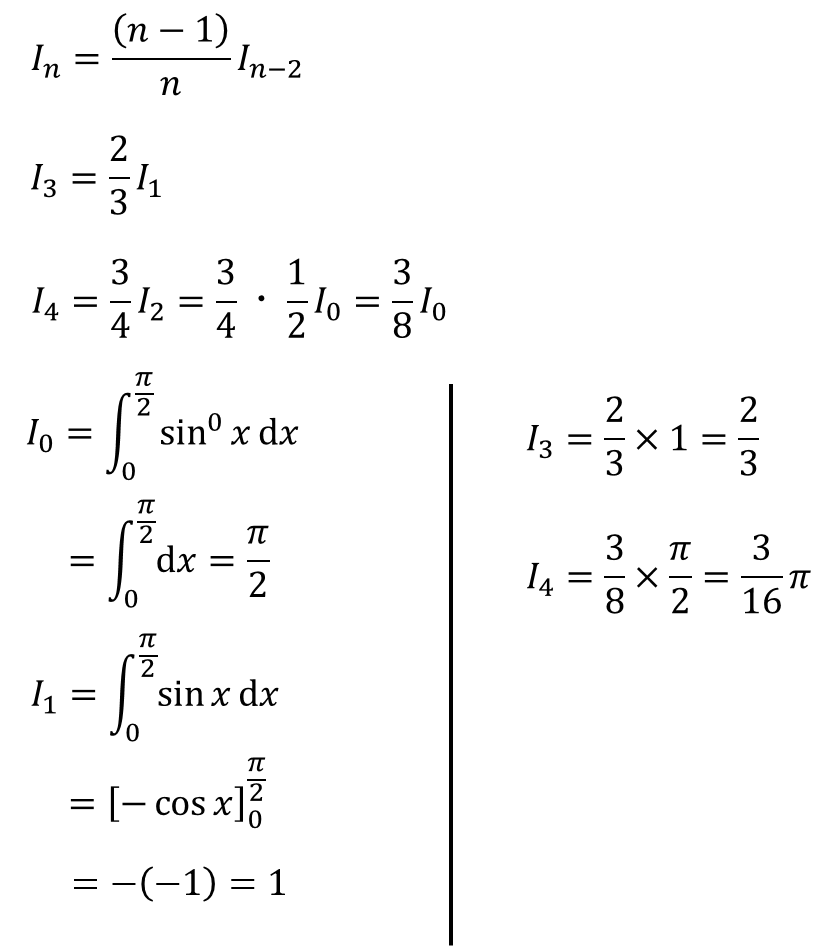

・・・おっけ。正解だ。おめでとう!

よかった~!
まとめ
今回は、部分積分とそれを使った具体的な問題の解法、そして色々ある過去問のうち、比較的基礎的な問題に触れてみました。
部分積分と三角関数を絡めた問題は、大学受験によく出てきます。
数学Ⅲが入試の範囲に入っている場合は、
・「積分・そのまま・マイナス・積分・微分」と10回唱えて
・微分役と積分役を意識して
部分積分に慣れてみてください。数学は慣れの積み重ねです。
部分積分を応用した、大阪大学の「πは無理数であることを証明せよ」という問題もやってみました。部分積分に慣れたら見てみてください。
[blogcard url=”http://shimaphoto03.com/science/pi-irrational/”]
 らい・ぶらり
らい・ぶらり



コメントを残す