資料請求番号:TS42
CONTENTS
F=maからのナビエ・ストークス式の導出
ここでは、流体の流れを表す方程式であるナビエ・ストークス方程式(以下、NS式)を古典力学および保存則から導出します。教科書に書かれているNS式の導出は記号を省略していることが多く、コンパクトですが、初学者には敷居が高いことが多いです。このページでは冗長になることを覚悟してなるべく記号を省略せずにNS式を導いていきたいと考えています。
ナビエ・ストークス式
NS式は以下の式で表されます。
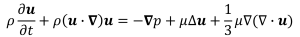
ρは流体の密度、uは流体の流速でベクトルです。u = (u, v, w) x方向の流速をu, y方向の流速をv,z方向の流速をwとしています。pは圧力、μは流体の粘度です。∂や∇などの記号はベクトル解析で出てくる記号で、偏微分、ナブラを意味します。
この方程式は実は3つの方程式がまとめて記述されており、この方程式にプラスして連続の式を連立して解くことによって、速度ベクトルu = (u, v, w) と圧力pを求めることができ、流体の振る舞いを予想することができるようになります。
※ここではベクトル解析の計算の基本ができることを前提としています。勾配、発散、回転ってなに??という方は先にこちら
導出
運動方程式 (力 = 質量×加速度)
F = ma。この運動方程式は基本ですよね。NS式は流体の運動方程式なのですから、例外なく、この式に従います。ただ、Fやらmやらaがほかの文字で色々置き換わっているだけのことです。NS式を導くということはF=maを流体の振る舞いにマッチするように書き換える作業と言えるでしょう。それではmから始めます。
質量
流体というものはその場その場で速度や圧力(変数)が変化するものです。ですから、小さい小さい箱を用意して、その中で保存則が成り立ち、その箱をいっぱい集めて流体を表現するという方法をとります。この小さい箱を検査体積と呼びます。
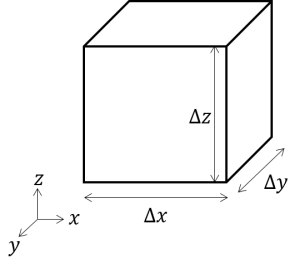
検査体積
この検査体積の質量は流体の密度がρだとすると
![]() (1-1)
(1-1)
となります。ひとまず、F=maのmの部分を表すことができました。
加速度
流体の振る舞いを表現するのに「ラグランジュの方法」と呼ばれるものがあります。これは流体を細かい粒子に見立てて、その場その場における粒子の物理量(速度など)を表現する方法です。粒子の物理量はその場、その時刻で変化しますから、物理量をfとすると
![]()
と表現することができます。そして、これの全微分を求めてみます。このとき
![]() であることに注意すると
であることに注意すると
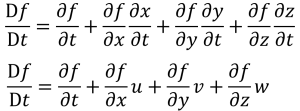 (2-1)
(2-1)
となります。この物理量fが速度uだったらどうなりますか?Du/Dtは加速度ですよね。
では、(2-1)式にuを代入してみましょう。
![]()
そうすると(2-1)式はベクトルになって、それぞれの方向の式が出来上がります。
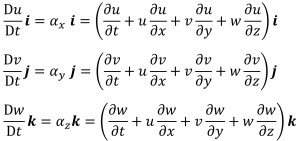 (2-2)
(2-2)
加速度ベクトルは
![]() (2-3)
(2-3)
ですね。
(2-2)式を一つの式にまとめようとするなら
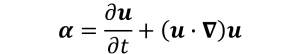 (2-4)
(2-4)
となります。
F = maのmaの部分は(1-1)式と(2-4)式から
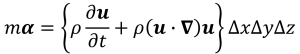 (2-5)
(2-5)
力
次にF =maのFの部分を流体に当てはめてみます。これが一番大変です。検査体積の流体にかかる力を整理しましょう。τで表されるせん断とσで表される圧縮があります。
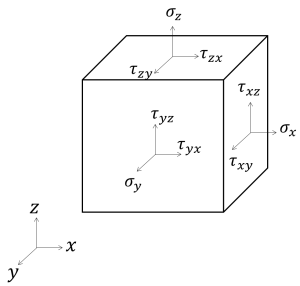
検査体積にかかる力
添え字について説明しますと、1番目の添え字は面、2番目の添え字は方向を表します。すなわちτyzはyの面にかかるz方向のせん断力を意味します。
そして、それぞれのせん断力、圧縮力は
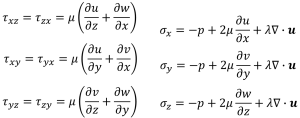 (3-1)
(3-1)
で表されます。検査体積にかかる圧力とニュートンの粘性の法則を基礎としています。
次に検査体積の表面にかかる力を計算します。x面だったらx+Δx面とx面にかかる力の差を取ることで、検査体積の表面にかかる正味の力を求めることができます。これをy面、z面について行います。
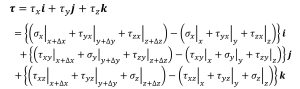 (3-2)
(3-2)
テイラー展開の考え方から、x+Δxとxの物理量の差分は物理量の偏微分で表現できます。
テイラー展開の考え方はこちらを参照
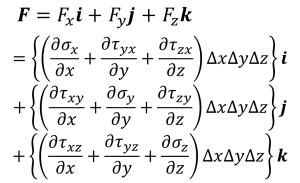 (3-3)
(3-3)
(3-2)から(3-3)の変形において、σxの例を見たい方はこちら
次に(3-3)式に(3-1)式を代入して整理します。
 (3-5)
(3-5)
一般的に圧力による歪みを表す粘性であるλは
λ = (-2/3)μ の関係があります。そして、uの発散∇・uは
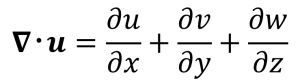 (3-6)
(3-6)
以上をもとに(3-5)式を変形すると
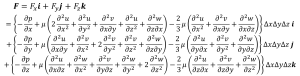 (3-7)
(3-7)
を得ます。さらに変形して
 (3-8)
(3-8)
を得ます。これで運動方程式F = maのFの部分を得ることができました。
運動方程式 F=ma へ代入
それでは、今までに得たm, a, Fの材料を合体して運動方程式にしてみましょう。
(1-1)×(2-2) = (3‐8)はこんな形になります。
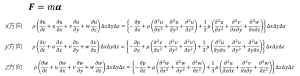 (4-1)
(4-1)
これを教科書に書いてあるような省略した形で書けば
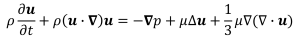 (4-2)
(4-2)
となります。
そして非圧縮性流体では
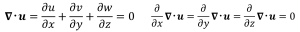 (4-3)
(4-3)
が成立するので、非圧縮流体のNS式は(4-1)式から変形して
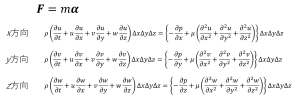 (4-4)
(4-4)
となります。省略して書けば
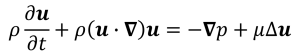 (4-5)
(4-5)
となります。
これでNS式の導出は終わりです。これを解けば身の回りにある流体(水や空気)の振る舞いを計算で求めることができるようになります。どう計算するかはまた別の(数値流体力学)のお話・・・。とりあえずはお疲れさまでした。
スポンサーリンクおまけ
NS式の厳密解の解き方は誰もわからない
今回導いた、NS式は解析解(厳密解ともいう)の解法が見つかっていません。解析解とは、例えば、dN/dt = -kNという式は変数分離を使って、積分して解くことができますよね。このように紙の上で、方程式の連続性を保ったままで方程式を解くことを「解析解を得る、あるいは厳密解を得る」といいます。NS式ではこれができないのです。
数値流体力学シミュレーション(CAE)
それではどうしているのでしょうか?離散化して代数方程式にして解いているのです。(dN/dt はN2-N1/Δtに近似できますね。そうすればdN/dt = -kNは代数方程式になりますね。)
これがCAEによる流体力学シミュレーションの基本的な考え方です。NS式では未知数が4個(p,u,v,w)あるのですが、式は3つしかありません。そこで、連続の式と連立させて解きます。
連続の式についての解説はこちら
大学や会社では、自分で一からコードを書くのではなく、シミュレーションソフトウェアを利用している場合が多いです。基本はシミュレーションソフトを使用し、研究や設計を進めるうえで、シミュレーションソフトで対応できない現象のモデル化をしたときに、コードを書きくわえたりします。シミュレーションソフトは一般的に高額でライセンス料が百万円単位だったりするのですが
驚いたことに無料で誰でもしようでいる数値流体力学シミュレーションソフトがあります。OpenFOAMといいます。無料ですから、サポートはもちろんなく、自分で使い方をマスターするしかありません。また、使い方もあまりユーザーフレンドリーではありません。ただし、ある程度使い方を知ることができれば、自宅でコンピュータシミュレーションができる!しかも無料で!という大変魅力的なソフトです。
OpenFOAMについてはこちら。LinuxOS上にOpenFOAMをダウンロード・インストールする方法を説明しています。
他の現象の基礎式
今回はNS式という、流体の振る舞いを表す基礎式を説明しましたが。本ブログには電磁気学のマクスウェル方程式、量子力学のシュレディンガー方程式についての解説もございます。興味があればぜひ覗いてみてください。
 らい・ぶらり
らい・ぶらり
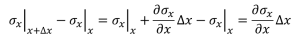 (3-4)
(3-4)





コメントを残す