資料請求番号:TS52
スポンサーリンク一言でいうと?
「物質の広がり方を表す方程式」
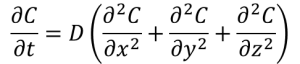 ・・・①
・・・①
方程式のイメージ
この方程式は例えば、
水槽の中にインクを入れたら、どんなふうに広がるのか?
というような問題に答える方程式です。「どんなふうに広がるのか?」を表現するから「拡散方程式」なのです。

基本的に物質は濃い方から薄い方へ移動していくんだ。
水槽の中にインクを入れたとき、インクが水槽全体に広がっていくことはあっても、
水槽全体に広がったインクが一部分だけ濃くなっていくことはないだろ?
拡散方程式を使えば、どのくらい時間が経ったら、どのくらいインクが広がっているのかがわかるんだ。
Cは物質の濃度[mol/L]、x,y,zは座標、tは時間を表します。∂は偏微分の記号です。
t=0におけるCの分布、つまりC(x,y,z,0)を与えて(これを”初期条件を与える”と呼びます)
この方程式を解けば
Cを時間tの関数と空間(x,y,z)の関数つまり、C(x,y,z,t)で表わすことができるので、
ある時間tにおける、ある場所(x,y,z)でのCの値を求めることができるのです。

ある時間、ある場所におけるCの値というのは、つまりどれだけ時間が経てば、どのくらいインクが広がっているかを現わしてるよな。

拡散方程式を使えばt=0の状態から未来のCの分布を予測できるわけなんだ。
そうやって考えるとなんだか魔法のような方程式な感じがしてこないか?
拡散方程式の導出
それでは、拡散方程式を導出していきましょう。
検査体積の物質収支
拡散方程式のような微分方程式を導出する際にはとても小さい空間での物理量(今回は濃度)のやり取りを考えます。今回は下図に示すような縦横高さΔx、Δy、Δzの空間を用意します。この空間のことを「検査体積」と呼ぶことがあります。
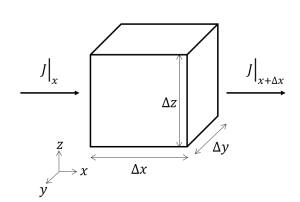
J(x)[mol・m-2・s-1]というのは単位時間、単位面積あたりに位置xから空間の中に入ってくる物質の量です。
※図ではJ(x)はJに縦棒立てて右下にxと示しています。これは教科書でもよくある書き方です。

J(x)にはs-1の単位があるな。そうするとJ(x)は単位面積あたりで空間へ物質が入る速さとも考えられるよな。
今、空間の中に断面積ΔyΔzを通ってJ(x)の速さで物質が入り、J(x+Δx)の速さで物質が出ていくと考えます。空間の中に物質がたまっていく速さ(∂C/∂t)ΔxΔyΔzは
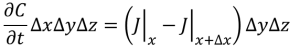 ・・・②
・・・②
で表わされます。

②の式のがイマイチ、ピンと来ない場合は身の回りの現象でイメージしてみるといい。
例えば、空間をお風呂と考えましょう。
風呂の栓を開けて蛇口を開きます。蛇口の開き具合が大きくてジャバジャバと水が入っていくほど(J(x)ΔyΔzが大きいほど)風呂の水は早く溜まっていきます。
ここで蛇口の閉めていきましょう。風呂の水が溜まる速さは遅くなっていき、今度は逆に水がなくなっていきます。
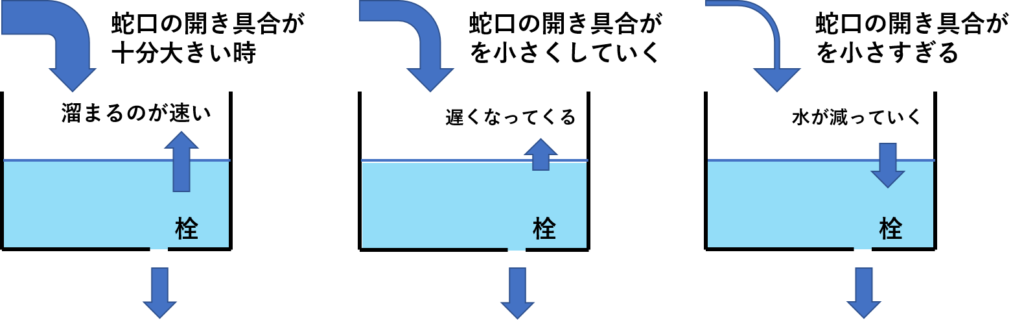

空間の中へ物質が出入りする速さは、
物質の溜まっていく速さと出ていく速さに効いてくる。
これがイメージ出来ればOKだ。
空間の中へ物質が出入りする速さ = 空間の中へ物質が入る速さ―空間の外へ物質が出ていく速さ
という考え方のもと②式が立てられます。②式を立てることを「物質収支をとる」と言います。

それから、②式の左辺と右辺の単位は必ず一致している。物質収支を立てる時はこれのチェックを欠かさずにやらないといけないんだ。
両辺の単位を検証してみましょう。
断面積ΔyΔzの単位はm2、J(x)の単位は[mol・m-2・s-1]です。ということはJ(x)ΔyΔzというのは断面積ΔyΔzを通って位置xから空間の中へ物質が入る速さです。単位は[mol・s-1]です。
同様にJ(x+Δx)ΔyΔzというのは断面積ΔyΔzを通って位置x+Δxから空間の外へ物質が出る速さです。単位は[mol・s-1]です。
左辺の(∂C/∂t)ΔxΔyΔzの「ΔxΔyΔz」は空間の体積です。濃度[mol・m-3]×体積[m3]は物質量[mol]ですね。これをtで微分しているわけですから、物質が溜まっていく速さ[mol・s-1]を表します。左辺と右辺で単位が合いました。これで方程式として成立します。

今回は与えられた方程式を検証したが、本来は自分で方程式を立てなければいけない。
そういったときに、方程式の右辺と左辺の単位は必ず一致している。という考えの下、現象と方程式の辻褄が合うように単位を揃えていくという作業を意識しておけば、
間違った方程式を立てずに済む。
これは以前紹介した「物理や化学の計算が簡単にできる方法」の応用編だ。
Jを濃度の関数で表現
②式に登場している、「単位面積あたりに空間に物質が入る速さ」Jというのを濃度Cの関数で表現してみましょう。
このJは「移動現象論とは?」の記事で詳しく解説しました。ここでもJは物質の移動する速さを現す式だと解説しています。
物質の移動の速さは「定数×濃度勾配」で表わされます。Dは拡散定数[m2・s-1]です。
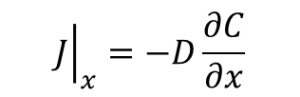 ・・・③
・・・③
式変形

物質収支②式を変形していこう。
出口での物質移動速度J(x+Δx)はテイラー展開で求められる。
そして②式に③式を代入して変形していけば拡散方程式は完成する。やってみよう。
まず、出口での物質移動速度J(x+Δx)ですが、テイラー展開と③式の代入で
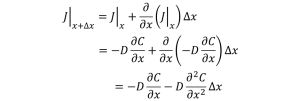 ・・・④
・・・④
のように変形できます。
テイラー展開は関数f(x)のxの周りではf(x+Δx)=f(x)+f‘(x)Δxが近似的に成り立つというものです。
次に、③式と④式を②式へ代入していきましょう。
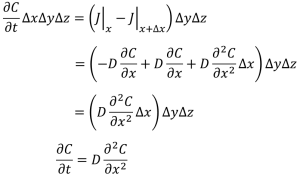 ・・・⑤
・・・⑤

これでx方向の拡散方程式は完成だ。
この調子でy方向、z方向も考えてみよう。
先ほどは一方向からしか物質が出入りしないと考えていましたが、y方向からもz方向からも物質が出入りすると考えます。
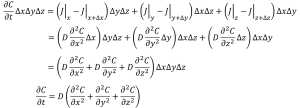 ・・・⑥
・・・⑥
これで拡散方程式の完成です。
まとめ
いかがでしょうか?最初、拡散方程式を見た時に、うわぁ・・と思った人がいるかもしれませんが、空間の中に物質が出入りするということを式にしただけなんです。
実際の現象をイメージし、単位に気を付けて「溜まる速さ=入る速さ-出る速さ」の式を組み立てていけば色々な微分方程式が立てられるようになります。
 らい・ぶらり
らい・ぶらり



わかりやすい
ありがとうございます
わかりやすいなあ
ありがとうございます