資料請求番号:TS11
CONTENTS

サイクロイドの媒介変数表示と描画
サイクロイド曲線と言えば以下のような媒介変数表示で表現できて
![]()
グラフの概形は以下のような形になる曲線のことを思い浮かべると思います。
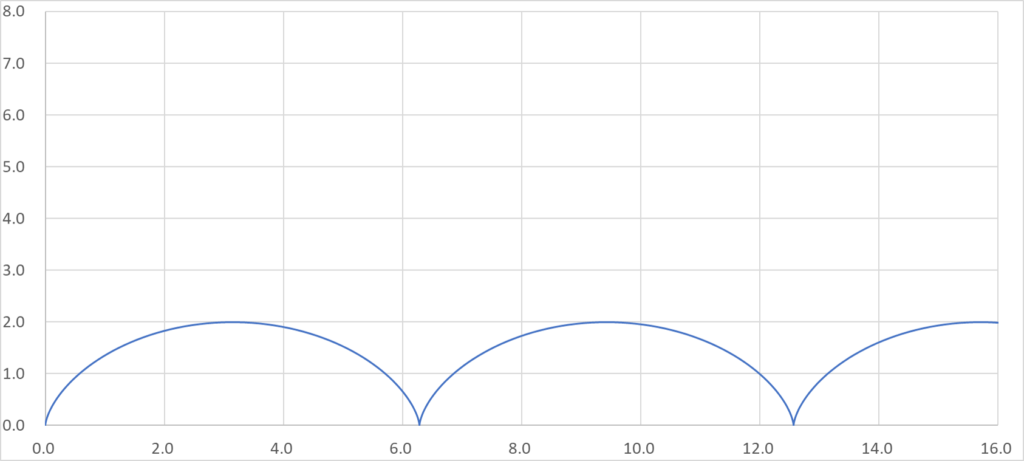
高校数学Ⅲでは、媒介変数表示された関数を与えられ、それを微分してグラフの概形を描いたり、積分して面積を求めたりする問題がよく出ます。
受験勉強に慣れた人はこの式を見るだけでグラフの概形を想像することもできるでしょう。
これに似た問題で、アステロイドという曲線の問題も頻出です。
![]()
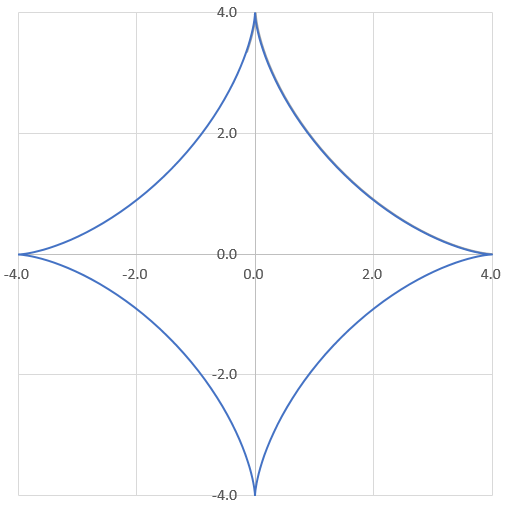
本記事では、サイクロイドやアステロイドがどのようにしてできる曲線なのかを詳しく解説し、色々なサイクロイドをエクセルを使って描画してみたいと思います。
※サイクロイド・アステロイドの式と曲線の形を確認したい方はこちら。式と概形だけをまとめてあります。
※描画例
サイクロイドとアステロイド
サイクロイド
まず、サイクロイドとはどのような曲線だったか、おさらいしておきましょう。
Wikipediaによると、
サイクロイド (cycloid) とは、円がある規則にしたがって回転するときの円上の定点が描く軌跡として得られる平面曲線の総称である。
出典:Wikipedia サイクロイド
とのこと。

もうな、この文章そのものが意味わからんねん!円上の定点が描く軌跡?なんのこと??

まぁまぁ。まず、円を描くやろ?

うん。


次に円の先っちょに点を打つたい。

うん。


これをな、直線上で転がすたい。

それで、赤い点が移動したやろ?赤い点を追いかけたら曲線ができるたいね。

つまり・・・赤い点の・・・轍のこと?

せや!この辺ば雪降らんが、長崎の方に行くとたまに降るやろ?その雪道を車走ると轍ができるやろ?
そういう、モノが通った跡のことを「軌跡」っていうたいね。
そのことを理解した上でもう一回、「サイクロイド」の定義を読んでみ?
サイクロイド (cycloid) とは、円がある規則にしたがって回転するときの円上の定点が描く軌跡として得られる平面曲線の総称である。
出典:Wikipedia サイクロイド

回転する円上の定点・・・つまり赤い点が、描く軌跡・・・つまり赤い点の轍・・・がサイクロイドってこと?

ああ。つまり、こういうことだな。
軌跡を残して描いたら、サイクロイドのできあがりってことたいね。

なるほど~!!
アステロイド

アステロイドがどんな曲線か覚えとる?

全然!!

・・・・。
以下のような媒介変数表示の式で表される曲線をアステロイドといい
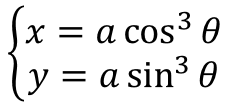
概形を描くと以下の様になる。


思い出した?

ああ、あのダイヤのやつな!

どうやって描くんか知らんけど・・・。

さっきのサイクロイド曲線は直線の上に円を転がしたやろ?

うん。

今度は円の中で円を転がすねん。

アステロイドっぽい・・・?

じゃあ、次は軌跡を残して描いてみるで。

おおっ!アステロイドや!!

ああ。アステロイドってのは
「円の中に半径1/4の円を描いたときに、円上の定点が描く軌跡」のことを言うたい。
サイクロイドとアステロイド まとめ
サイクロイドとは、直線上を回転する円上の定点が描く軌跡。
アステロイドとは、円Aと円Aの半径1/4の円Bがあるとき、円Aに円Bを内接させ、回転させたときに円B上の定点が描く軌跡
広義のサイクロイド
内サイクロイドと外サイクロイド

それでな、高校の数学ではな、直線上で円を転がして出来た曲線の事だけをサイクロイドと言うが、実はアステロイドもサイクロイドの一種たい。

どういうこと?

もう一回、サイクロイドの説明を見てみ?
サイクロイド (cycloid) とは、円がある規則にしたがって回転するときの円上の定点が描く軌跡として得られる平面曲線の総称である。
出典:Wikipedia サイクロイド

円がある規則に従って回転する時・・・・ってあるやろ?
直線上を円が回転しようが、円の中を円が回転しようが、
円がある規則に従って回転していることには変わりはないたい。

つまり・・・デッカイ円の中でチッサイ円が回転することを規則と考えりゃ、アステロイドもサイクロイドの一種ってこと?

せや!せやから、
高校数学でいうサイクロイドってのは
直線上に円を回転させてできるサイクロイド、
アステロイドってのは
円の中の円を回転させてできるサイクロイド
っていう表現ができるたい。もう一回、サイクロイドとアステロイドのイメージ動画を観てみ?

・・・・なるほど~。

円の中の円を回転させてできるサイクロイドで特に半径比が4:1の場合をアステロイドっていうたい。一般的には他にも別名があってな
ハイポサイクロイドとか、内(ない)サイクロイドとか言ったりするたい。

内サイクロイド??

ってことは、外(がい)サイクロイドもあるってこと?

せやせや!描いてみるか?

うん。

ある円に対して、半径が1/3の円を用意して、円の周りを転がすたい。

すご~い!お花模様みたいでかわいい!
エクセルを使って多様な図形を描く
内サイクロイド(ハイポサイクロイド)

これさぁ・・・。円の内でも外でもええけど、小さい方の円の大きさ変えたら色々な図形が描けると?

おおっ!ええこと気づいたな!例えば、内サイクロイドであるアステロイドは媒介変数表示でこんな式やけども
![]()

これを3倍角の公式を使って式の形を変えると、こうなるんや。
![]()

この3をな、nに置き換えて、nを色々な数字に変えると色んな図形が描ける
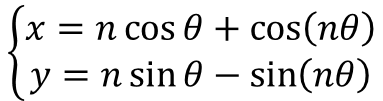

nが2のとき、半径1/3の円を転がしたときの軌跡ができるたい。
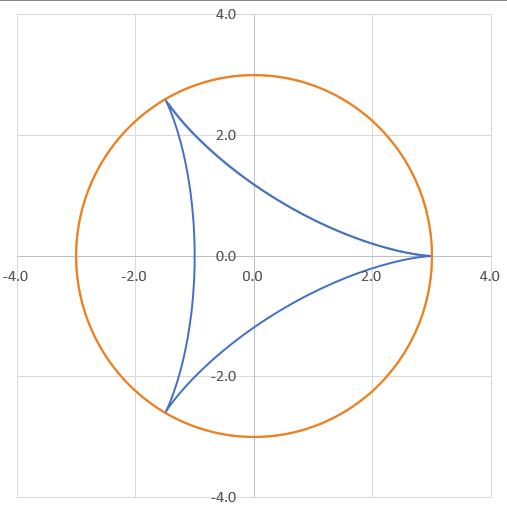

nが3のとき、半径1/4の円を転がしたときの軌跡ができる。これがアステロイドだったやろ?
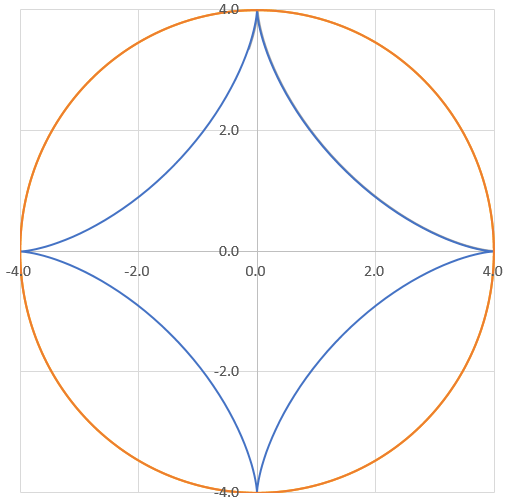

こういうふうに、上の式に従ってnを変えると、1/(n+1)の円を転がしたときの軌跡ができるたい。

えっと・・・n=3のときに半径1/4の円を転がして、ダイヤみたいなマークが出来たってことは・・・

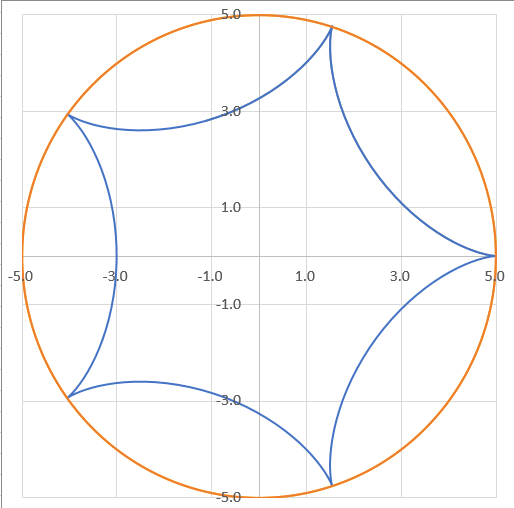
えっと・・・n=4のときに半径1/5の円を転がして、星みたいなマークができると?

せやせや!なかなか柔軟なアタマしとるなぁ~!

へへっ・・。それでね、nをめっちゃ増やすとめっちゃトゲトゲができるけんね!

(・・・かわいいなぁ。)
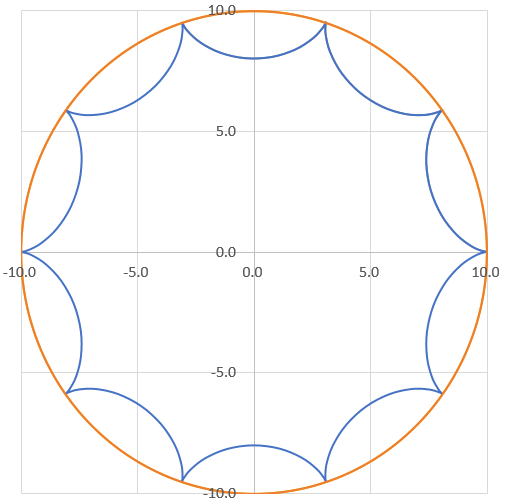
(左:n=4 星型,右:n=9 めっちゃトゲトゲ)

nを1から100まで変化させてグラフを描くとこんな感じ

うお~っ!めっちゃトゲ増えよってん!!
最後に円になるってのも、おもろいな!

せやな!どんどんドゲが細かくなっていくからな。
それでな、もっとおもろいのがな、nを小数点にするとな・・・

え~なにこれ!すご~い!
n=1.5とか、めっちゃ星やん!!
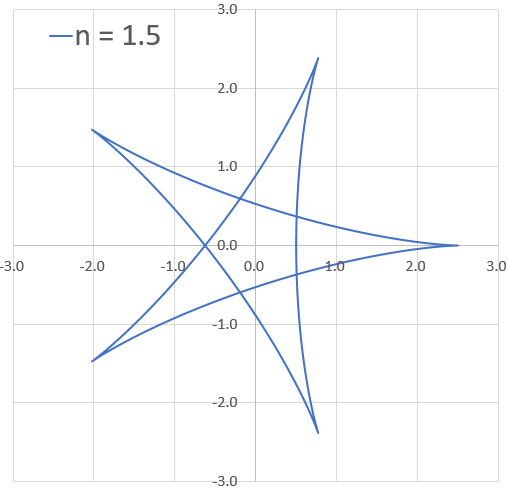

これでアタシ、数式で星描けるけん!って自慢できる~♪

(さらに言うと、バラ曲線にフーリエ級数を仕込むとサクラの花びらまで表現できるんだが・・・まぁいいや。)

ちなみにだが、内サイクロイドはこういう形の式でも表現される。
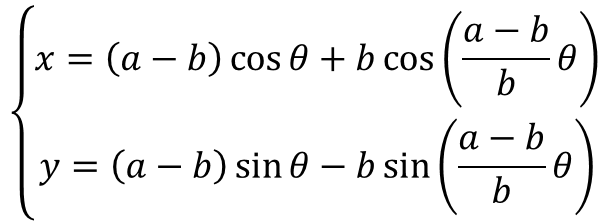

この数式使ってな、「半径aの円の内周を半径bの円が転がるとき、半径b上の定点が描く曲線を内サイクロイドという」という表現できるたい。

えっと・・・半径aがデッカイ方で半径bがチッサイ方やけんね?

せやな。

やとしたら・・・

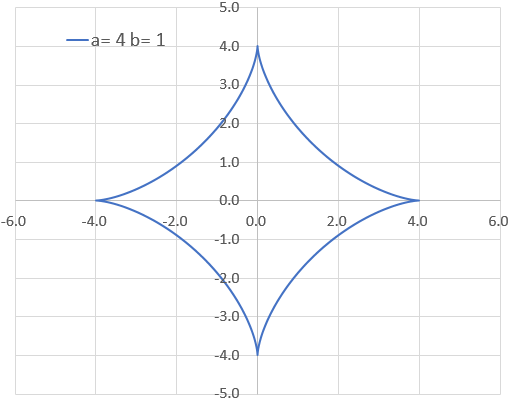
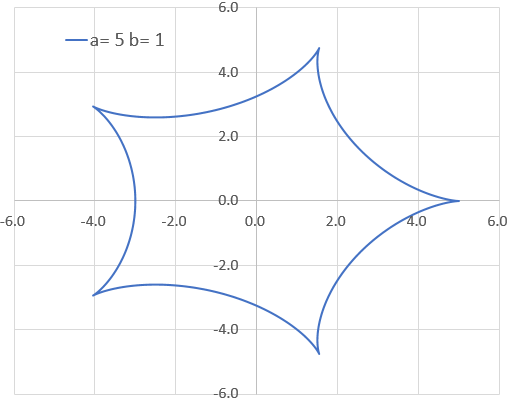
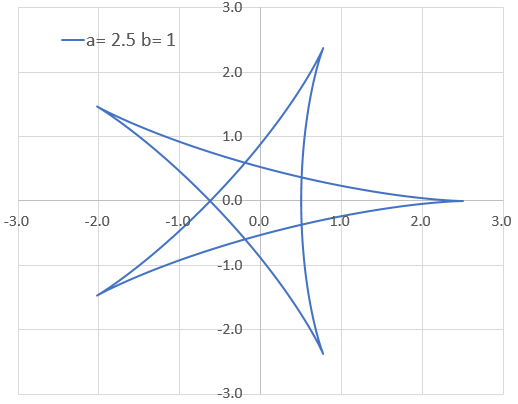
aが4で、bが1ならダイヤのマークでaが5でbが1とか、aが2.5でbが1とかなら星のマークになるけん!

せやせや!ダイヤのマークはアステロイドな。

・・・・♪

(・・・やっぱりかわいいなぁ。)
外サイクロイド(エピサイクロイド)

さっき、円の外に小さい円を置いて転がした軌跡でお花みたいな形を描いたやろ?

うん。

これもな、円をある規則に従って回転させとるけん、サイクロイドって言うけど、この場合を特に外サイクロイド、エピ・サイクロイドって言うたい。

これも、4つ葉のお花とか5つ葉のお花とか描けると?

描ける。外サイクロイドの式は以下の通り。
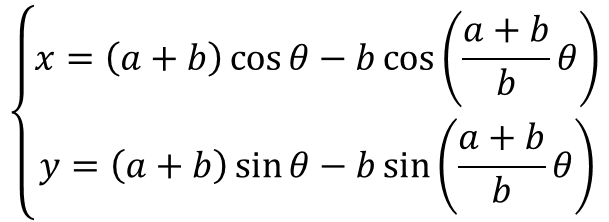

この数式使ってな、「半径aの円の外周を半径bの円が転がるとき、半径b上の定点が描く曲線を外サイクロイドという」という表現できるたい。

また100個描いてみようよ!

お~すごか~!

これもまた、aを小数点にすると、色々な形が描ける。

お~幻想的~!
こんなん学校の授業じゃ見せてくれんから、すごくおもろいわ~!

そっか。それは良かった。ちなみにaもbも1のとき、どんな形やった?
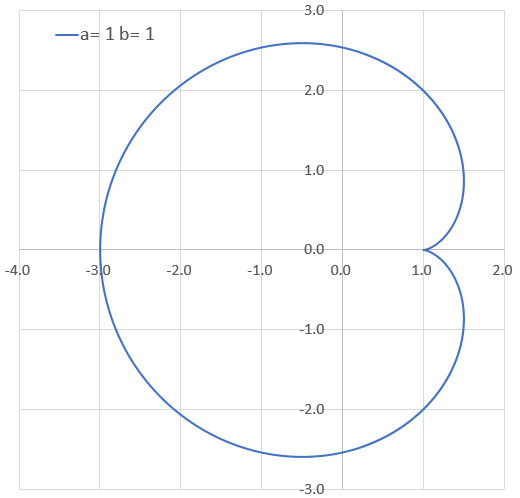

どっかで見たことがあるような・・・?

カージオイドやろ?心臓形。

ああっ、カージオイドもあったような気がする。カージオイドもサイクロイドの一種やったんか~!
まとめ
本記事では、高校数学で習うサイクロイドとアステロイドの説明をした後、色々なサイクロイドについて説明し、描画しました。
サイクロイド (cycloid) とは、円がある規則にしたがって回転するときの円上の定点が描く軌跡として得られる平面曲線の総称である。
出典:Wikipedia サイクロイド
サイクロイド:円が直線の上を回転する時の円上の定点が描く軌跡として得られる平面曲線
内サイクロイド・アステロイド・ハイポサイクロイド:
円が他の円の内周を回転する時の円上の定点が描く軌跡として得られる平面曲線
外サイクロイド・カージオイド・エピサイクロイド:
円が他の円の外周を回転する時の円上の定点が描く軌跡として得られる平面曲線
式と概形の関係は以下の記事にまとめました。
また、他にもリマソン、バラ曲線など色々な曲線の媒介変数表示をまとめました。こちらも併せてどうぞ!
数式さえあれば、エクセルに入れて簡単に計算できるので、やってみてはいかがでしょうか?
※動画はマクロを使って作りました。マクロの描き方は後日公開したいと思います。
 らい・ぶらり
らい・ぶらり
コメントを残す