資料請求番号:TS11

エクセルを使って曲線をグラフィカルに表現してみた
以前、高校数学で出てくるサイクロイドとアステロイドを紹介しました。
※例:内サイクロイド
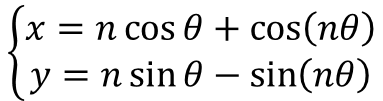
本記事では、様々な曲線を媒介変数表示(※)で紹介します。紹介するだけの記事です。
※エクセルで描くことを想定し、媒介変数表示にしています。

こないだの星描いたり、バラの絵みたいなの描いたりするの楽しかった~!他にこういう曲線てないの?

あるぜ。とりあえず、蝸牛線/対数らせん/リサージュ曲線/正葉曲線を紹介しようか。
パスカルの蝸牛線(リマソン)
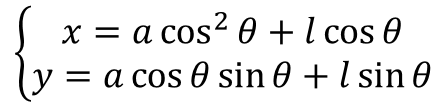
定数と曲線の形 a = 0~10 0.1刻み, l = 2 → a=10, l = 2~0 0.1刻み
リアルタイム描画 θ = 0π~2π(a = 6, l = 2)

なんか、カタツムリみたいやね。

お、ええとこ気づいたな!「かぎゅう」は漢字で書くと「蝸牛」。これはカタツムリを漢字で描いてもこの漢字になるたい。

動物の模様が数式で表現できるってすごか~!

動物の模様を大真面目に数学で考えている人や動物の生命活動を数学で理解しようとしている人は実際におって、そういう人たちを数理生物学者って言うたい。

ふぅ~ん。
対数らせん
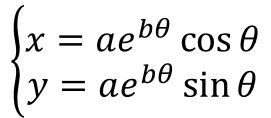
定数と曲線の形 a = 1, b = 0.01~0.5 0.01刻み → a = 1,b = 0.5~0.01 0.01刻み
リアルタイム描画 θ = 0π~6π(a = 1, l =0.3)

デッカなったり、チイサなったり忙しいねぇ。リアルタイム描画なんかは最初動きが小さすぎて、再生しているのかどうかわからんかった。

まぁ、対数やからな。
リサージュ曲線
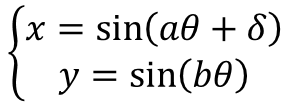
定数と曲線の形a = 1~20 1刻み, b = 8
※δ=πとしています。

うわ~っ!これすご~い!!不思議や~!!

これは俺も凄かな~思うてる。構成しとるのは単なる振動で、位相をずらすだけやのにこんなに単純な形になったり複雑な形になったりするんやなぁ~

アタシ、6番目のヤツが好いとうね!なんかこう、宇宙人のマークみたいや!
リアルタイム描画 θ = 0π~2π(a = 6, b =8)

いや~17番目も捨てがたいやろ。数学で表現する編み物みたいな感じがええなぁ~。
リアルタイム描画 θ = 0π~2π(a = 17, b =8)
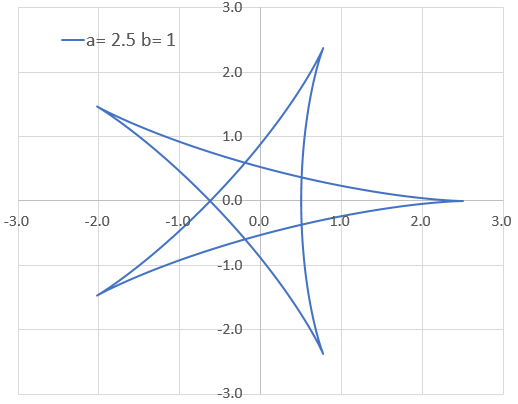
正葉曲線(バラ曲線)
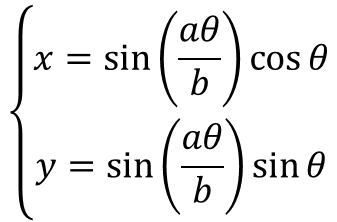
定数と曲線の形a = 1→8 1刻み,b = 1 → a = 8, b = 1→8 1刻み

うわ~っ!キレイ~!!2番目のやつなんか好いとうよ!
リアルタイム描画 θ = 0π~2π(a = 2, b =1)

a=2,b=1の四つ葉か。ええなぁ。
この正葉曲線、別名バラ曲線言うんやけど、これを応用すると色んなものが描けるたい。
フーリエ級数使って花びらを表現したりしてな。

へぇ~。その、ふーなんとかを使えば色んなもんが描けるんやなぁ~!!

リサージュ曲線やバラ曲線なんかは、色々な定数を組み合わせると、ロゴマークかなんかのデザインができそう!
 らい・ぶらり
らい・ぶらり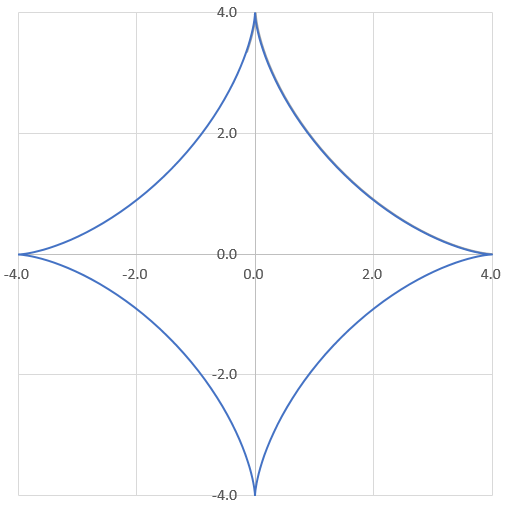
コメントを残す