資料請求番号：TS71

平衡移動を熱力学量で表現する～van’t Hoff式の導出～

高校化学の「化学平衡」の単元で「ルシャトリエの原理」と呼ばれるものを学習します。化学平衡については、本サイトでも取り扱っており、↓こちら↓にて詳しい解説があります。

 らい・ぶらり 

化学平衡の法則と問題例～高校化学をわかりやすく～

http://shimaphoto03.com/science/chem-equi/

資料請求番号：TS14化学平衡とルシャトリエの原理化学平衡は高校化学の中で比較的理解が難しい部類になるのでは、と思っております。化学の中でも計算量が多くあるうえに、どのように手を付けたらわからないという方もいると思います。本記事では、まず化学平衡とは...

このページの中で、化学平衡およびルシャトリエの原理を、以下のように著者間の会話を織り交ぜながら説明しました。

可逆反応が平衡状態にあるとき、濃度・圧力・温度などの条件を変えると新しい平衡状態になり、これを平衡移動といいます。その平衡移動は条件変化の影響を打ち消す方向に起こります。これをルシャトリエの原理といいます。

教科書的にルシャトリエの原理を説明すると、上記のような感じになります。それでは、平衡移動とは何なのでしょうか？ルシャトリエの原理をどのようにイメージしたらいいでしょうか？
「発熱反応において加熱すると平衡は左(反応物側)へ移ること」を例にルシャトリエの原理のイメージをまとめてみました。

化学平衡を習い始めたときにルシャトリエの原理ってのをやったやろ？

やった。条件を変えたら、その条件が打ち消す方向に平衡移動することやろ？アタシ、この問題は得意やけん。

じゃあ、この問題は？

N₂ + 3H₂ ↔ 2NH₃ + 92.2 kJの反応が平衡状態にあるとき
(1)温度を上げる
(2)圧力を高くする
(3)NH₃を除く
と平衡は左右どちらに移動するか

出典：数研出版編集部編，『改訂版　リードα 化学Ⅰ+Ⅱ』，改訂版第4刷，pp.170，(2006)

これはな！(1)が左、(2)が右、(3)が右や！

正解！

N₂ + 3H₂ ↔ 2NH₃ + 92.2 kJの反応が平衡状態にあるとき
温度を上げると平衡は左へ移動するのです。高校化学では、正反応が発熱反応であるため、温度を上げるとそれを打ち消す方向、すなわち逆反応側へ平衡が移動するというような習い方をしたかと思います。

今回は、大学で学習する「物理化学」「化学熱力学」に基づいて、このルシャトリエの原理を数式を以て定量的に表現する式を紹介します。そして、その式を化学熱力学の定義および定理を用いて導出してみたいと思います。

平衡定数の温度依存性を表す式　van’t Hoff式

今回は、結論から先にお話ししたいと思います。
化学熱力学の理論に基づいてルシャトリエの原理を定量的に説明する式は「van’t Hoffの式」と呼ばれ、以下の式で表現できます。

この式をグラフで図示すると、以下のようになります。

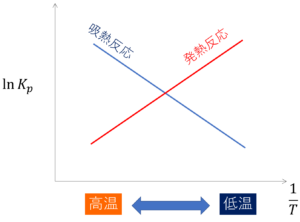
縦軸をlnK_p, 横軸を1/T（Tは絶対温度）のグラフをとると、勾配-ΔH゜/Rの直線が得られます。（厳密にいえば線形にならない場合もありますが、今回はこのことについては触れないでおきます。）
実験にてある反応温度Tにおける平衡定数K_pを求めることにより、その反応の反応エンタルピーΔH゜を計算することが一般的の使い方とされております。

このグラフを使用してルシャトリエの原理を説明することができます。

①このグラフはΔH゜が正のとき、すなわち吸熱反応の場合、右下がりになり、
ΔH゜が負のとき、すなわち発熱反応の場合、右上がりになります。

②一方、A+B⇔Cの平衡反応があった場合、気相反応ならば平衡定数は

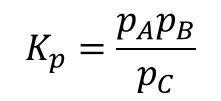
液相反応ならば

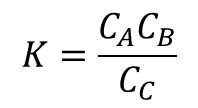
で表すことができます。

この①、②から、吸熱反応のとき、温度が上がれば上がるほど、平衡は右に進み、
発熱反応のとき、温度が上がれば上がるほど平衡は左に進むことが理解できます。

※グラフ上ではx軸が1/T、つまり逆数になっていることに注意してください。

van’t Hoff式の導出

このグラフが表す式、van’t Hoff式によって、発熱反応は高温にするほど平衡が左に進む、またはその逆を説明することができるようになりました。

それでは、このvan’t Hoff式を熱力学の定義とそれに基づく定理を用いて導出してみましょう。

 導出材料

①ギプスの自由エネルギーの定義
ギプスの自由エネルギーは、系の内部エネルギーのうち、私たちが系が行う仕事として自由に取り出せるエネルギーの最大量を表した物理量で、以下のように定義されます。

②自由エネルギーの全微分式
ギプスの自由エネルギーはTとPの二変数関数であるとして、全微分形式を求めると以下のようになります。

これを導出しようとすると、長くなるので割愛します。
各物理量の全微分形式は以下に示すような「熱力学関数の四辺形」で図解的に得ることができます。

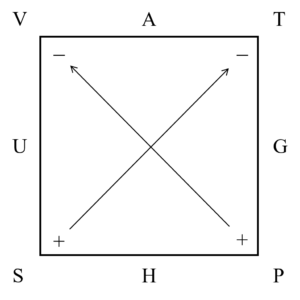
③自由エネルギーと平衡定数
化学反応に伴う自由エネルギー変化と化学反応の平衡定数との間には以下の関係が成り立ちます。

以上、①～③を２つのグループに分けて、導出を進めます。

グループ1の変形 Gibbs-Helmholtzの式の導出

(1-2)式を圧力一定として温度で微分すると

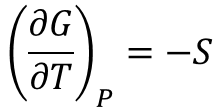
これを(1-1)式へ代入して、両辺をT²で割ると(1-3)式が得られます。

一方、G/Tを温度で偏微分します。数学Ⅲで学習する合成関数の微分の公式を用いて微分するのですが、GはTの関数であること(=Gは定数でない)に注意しながら微分を進めていきます。
この操作で得られる式を(1-4)式とします。

(1-3)の赤枠で示した部分と(1-4)の赤枠で示した部分は同じ関数であることに注意すれば

(1-5)式が得られます。これをGibbs-Helmholtzの式と呼びます。

Gibbs-Helmholtz式の利用

(1-5)式について、現在は化学反応を取り扱っており、標準状態を基準に熱力学量を相対的な物理量として取り扱っているということを考慮するとGibbs-Helmholtz式は以下のように書けます。

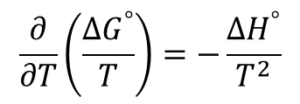
これに(2)式を代入すると

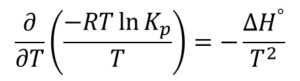
が得られます。これの式変形でvan’t Hoff式が導出できます。
まず、この時点で-RTlnK_pという物理量は温度だけの関数になるので、常微分方程式として取り扱うことができます。

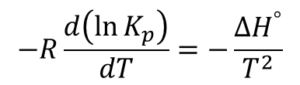
この常微分方程式をT₁~T₂まで積分して(2-2)式を得ます。

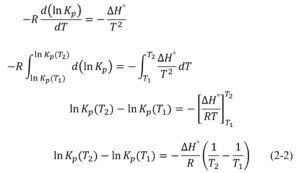
(2-2)式は平衡定数から反応エンタルピーを求める手段として有効です。

両辺温度項で割り、極限をとると、van’t Hoff式が得られます。

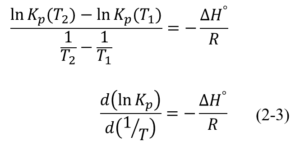
まとめ

今回は、高校化学で学習する「ルシャトリエの原理を定量的に理解する」ことを目標に、大学で学習する「物理化学」「化学熱力学」に基づいて、このルシャトリエの原理を数式を以て定量的に表現する式としてvan’t hoffの式を紹介しました。

このvan’t hoffの式は実験的に求められた圧平衡定数から反応エンタルピーを求めるのに有効です。一般的にはこのような使い方をするのですが、この式はルシャトリエの原理の説明そのものであるということを感じたので、今回、資料としてまとめることにしました。

van’t hoffの式はギプスの自由エネルギーの熱力学的定義および全微分式、平衡定数との関係式から導出することができ、この資料では導出過程を示しました。