資料請求番号:TS81
スポンサーリンクシュレディンガー方程式を解いて電子軌道を求める
電子の軌道には1s,2s,・・と言った名前がついていて、その中に電子が2個入るというように無機化学やら物理化学の授業で習ったかと思います。私のブログでも電子軌道の考え方を使って物質が光を吸収すること(吸光)、吸光によって物質が色を出すことを説明しました。
それでは、1sやら2sやらそういった電子の軌道の考え方はどのようにして生まれたのでしょうか?この記事では、これら軌道の考え方はどのようにして生まれたのか、すこし量子化学の領域に入って深堀りしてみたいと思います。
吸光についてはこちら
[blogcard url=”http://shimaphoto03.com/science/absorption/”]
吸光によって物質が色を出すことについての説明はこちら
[blogcard url=”http://shimaphoto03.com/science/leaf/”]
※この記事ではgnuplotと呼ばれる描画ソフトを利用しています。gnuplotの説明と使い方はこちら
[blogcard url=”http://shimaphoto03.com/science/gnuplot/”]
シュレディンガー方程式
方程式の形と意味
当ブログでは運動方程式を基礎とした流体力学の方程式、ナビエ・ストークス式の導出↓を行いました。このとき、
[blogcard url=”http://shimaphoto03.com/science/ns-equation/”]
・流体は流体粒子の集合体である
・流体の運動は速度ベクトルと圧力によって求められる
と説明しました。
ところが、電子の軌道と言った、原子の中の世界を見るためには、運動方程式のような古典力学の考え方とは異なる考え方が必要になります。それは
・電子は粒子であり、波である
・電子の運動は確率でしか予想することができない
という考え方です。これら基礎としたものが学問が量子力学であり、その基礎方程式がシュレディンガー方程式なのです。つまり
古典力学の基礎方程式→運動方程式
量子力学の基礎方程式→シュレディンガー方程式
ということです。
シュレディンガー方程式はこんな形をしています。
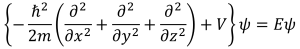 (1-1)
(1-1)
この式は光の粒子性と波動性を結び付けるド・ブロイ波の考え方からシュレディンガーが導き出した、電子の振る舞いを表す方程式なのです。シュレディンガーがどのように考え、この式を導いたのかの詳細はここでは割愛します。
各種記号の説明をします。hに線がついたような記号は「デイラック定数」と呼ばれ、プランク定数hを2πで割った数値となっています。(量子力学を勉強している人の間ではよくエイチ・バーと呼ばれています。)プランク定数と言えば、光の光子一つが持つエネルギーと光の振動数とを結ぶ比例定数です。(詳しくはこちら↓)
[blogcard url=”http://shimaphoto03.com/science/emw/#wave”]
mは電子の質量です。Vが電子のポテンシャルエネルギーで、Eが電子の持つエネルギー全体(運動エネルギー+位置エネルギー)、ψは波動関数です。
()内がラプラシアン演算子です。{}内をまとめてハミルトニアン演算子と呼びます。記号の説明は以上です。
大事なのは記号の意味を覚えることよりもこの方程式を解くことによって何がわかるか?です。その答えは「電子の状態」です。状態というのは具体的に言うと、どのくらいのエネルギーを持っていて、どこにいるのかということです。
先ほど、ψは波動関数ですとしれっと書きましたが、これがシュレディンガー方程式の解になります。波動関数は喩えるならば「流体力学の世界における位置ベクトルに相当する物」です。ただし、先ほど申したように電子の運動は確率でしか予想することはできないので、とある場所に電子がいる確率を表すものとなります。
とある体積dV=dxdydzをとり、そこに電子がいる確率を波動関数で表すならば
![]()
となります。つまり、シュレディンガー方程式を解くというのは「電子はどこにありそうか?」ということを探る作業になります。その答えが「電子軌道」というわけです。
シュレディンガー方程式を解く
ここから、シュレディンガー方程式を解く作業に入ります。一般的に、大学の授業では、仮定を大量において紙とペンを使って常識的な試験時間内に解けるように簡単にした「一次元井戸型ポテンシャル」を解くことになりますが、ここでは、現実の現象とイメージを結び付けやすいように、仮定をあまり置かない(=解くことが難しい)方程式に挑戦します。・・・と言っても、難しい数学的な式変形は飛ばして、どんな手順(アルゴリズム)で解くのかを説明するのに注力することとします。
座標変換
まず、式(1-1)はデカルト座標です。原子というのは球体ですので、座標系を球座標へ変換するとよいでしょう。ラプラシアン演算子の球座標変換は(2-1)で表されます。
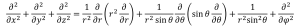 (2-1)
(2-1)
これを(1-1)式に適用して、右辺を0の形にすれば(2-2)式ができます。
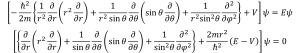 (2-2)
(2-2)
変数分離
次に偏微分方程式を解く常套手段である変数分離に移ります。まずは(r,θ,φ)を(r)と(θ,φ)に分離します。新たな変数RとYを定義して
![]() (2-3)
(2-3)
(2-2)式に代入して変数分離を施します。そうすると、(2-2)式はRに関する(2-4)式とYに関する(2-5)式に分離できます。ここで出てきたλは(r,θ,φ)いずれにも依存しない定数です。
 (2‐4)
(2‐4)
![]() (2-5)
(2-5)
次いで、(θ,φ)を(θ)と(φ)に分離します。新たな変数ΘとΦを定義して
![]() (2-6)
(2-6)
(2-5)式に代入して変数分離を施します。そうすると(2-5)式はΘに関する(2-7)式とΦに関する(2-8)式に分離できます。ここで出てきたνは(r,θ,φ)いずれにも依存しない定数です。
こうして、(2-2)式を、R(r)に関する(2-4)式とΘ(θ)に関する(2‐7)式とΦ(φ)に関する(2-8)式に分離しました。
![]() (2-4)
(2-4)
![]() (2-7)
(2-7)
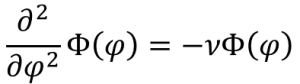 (2-8)
(2-8)
変数分離した方程式を解く
次に、変数分離して得た方程式をそれぞれ解きます。今回の目的は電子軌道の形を求めることなので、Rに関する式は解かずにΘとΦに関する式を解きます。数学的手段はさておいて、(2‐7)式を解くと、(2-9)式が得られます。
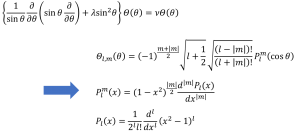 (2-9)
(2-9)
途中、mとかlとかいう記号が現れましたが、これは整数です。この方程式の解はlやmの整数倍の値しかとることができない(連続でない)ということを物語っています。
Φに関する方程式を解くと、(2-10)式が得られます。
 (2-10)
(2-10)
こうして出てきた二つの解Θ(θ)とΦ(φ)を掛け合わせたものを球面調和関数といい、これが電子の存在確率を表す関数となります。
球面調和関数
![]()
シュレディンガー方程式を解く手順 まとめ
シュレディンガー方程式というのは複雑でx+5 = 2 → x = -3のような簡単なアルゴリズムで解けるものではありません。以下の図にこれまで行ってきた手順(アルゴリズム)をまとめてみました。
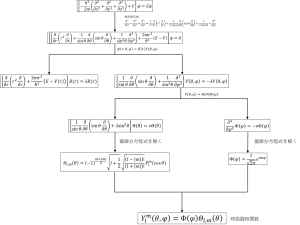
球面調和関数と電子軌道
球面調和関数の定義をもう一度示します。球面調和関数は極座標表現のシュレディンガー方程式を変数分離し、Φ方向の解とθ方向の解を掛け合わせたものになります。
![]() (3-1)
(3-1)
YやΘにl,mが付いているのがわかりますね。これは(2-9)式にあるl,mに色々な整数を代入して、色々な形状の関数Yが得られるという形になっています。逆に言えば関数Yはある決まった形にしかならないとも言えます。
さらに、Θに代入できるl,mには以下のような制限があります。
l = 0,1,2,・・・
m = 0, ・・・, ±(l-1),±l
例えば、l =2だったら、m = -2, -1, 0, 1, 2の数値しかとれないということを言っています。
具体的にl = 0 から l = 2まで(2-9)式と(2-10)式に代入して(3-1)を求めると、以下の式が得られます。
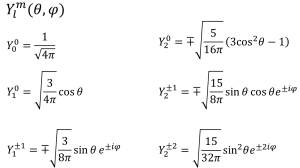
これらをgnuplotと呼ばれる描画ソフトで関数の形を描くと、以下の様になります。
※gnuplotの使い方はこちら
ただし、電子軌道というものは、波動関数の絶対値の2乗で表せる確率分布ですから、下記の演算処理をしています。
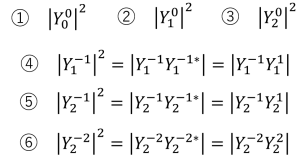
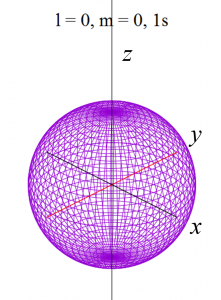 ①
①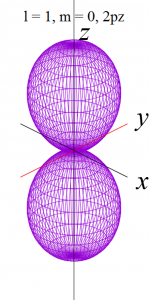 ②
②
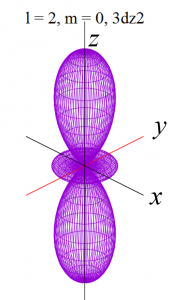 ③
③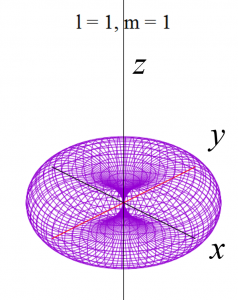 ④
④
 ⑤
⑤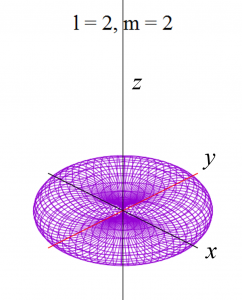 ⑥
⑥
さらに、球面調和関数を線形結合することで、大学でよく目にするような電子軌道を得ることができます。
s軌道
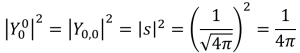

p軌道
px軌道
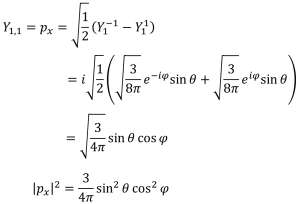

py軌道
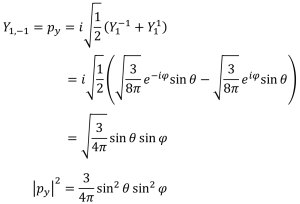
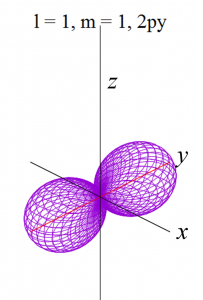
pz軌道
![]()

d軌道
dxy軌道
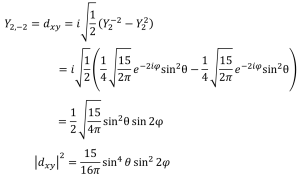
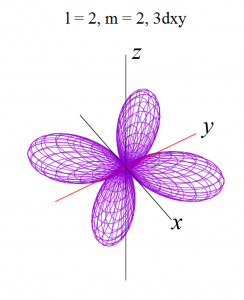
dyz軌道
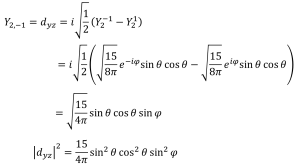
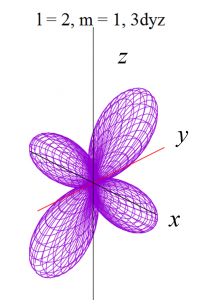
dz2軌道
![]()

dxz軌道
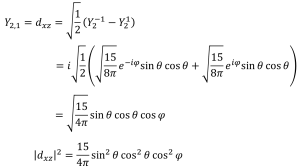
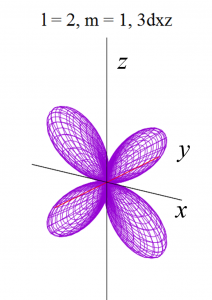
dx2-y2軌道
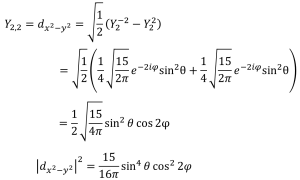
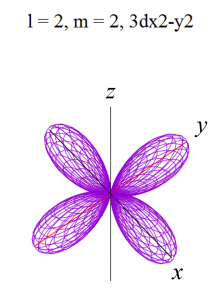
なぜ大学の授業で習う、s軌道・p軌道・d軌道の形がこんな風な形になるのか?これはシュレディンガー方程式の解が教えてくれることだったのです。
シュレディンガー方程式の解ψ(今回は変数分離してYの形になっています)は電子の存在確率を表してくれるということ、つまり電子がどこにありそうか?を教えてくれるということです。これがすなわち電子軌道なのです。
球面調和関数のlが0のとき、s軌道、l=1のときp軌道、l=2の時d軌道・・・に対応しています。このlを方位量子数と呼ぶと習った方も多いかと思います。球面調和関数とはθ方向とΦ方向の解ですので、方位量子数と呼ばれるのも納得ですね。
以上で、シュレディンガー方程式から電子軌道の考え方を知り、さらに電子軌道を、方程式を解いて求めて描画しました。とりあえずはこの記事の目的は終わりなのですが、上記の知識を使って私の記事ルビーはなぜ赤色なの?の補足説明をしたいと思います。
[blogcard url=”http://shimaphoto03.com/science/ruby/”]
おまけ(ルビー赤色の秘密)
電子軌道への電子の入り方(クロムイオンを例に)
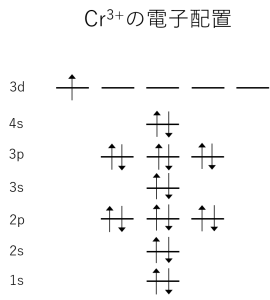
もう一度、クロムイオンの電子配置を見てみましょう。1s, 2s・・と書かれたsとpの意味はもう分かりますね。軌道の形を表しています。その前の数字は主量子数と言って、変数分離したときのR(r)の方程式(2-4)式を解くと現れる整数nで、電子軌道の半径方向の位置を表します。高校化学ではK核、L核、M核・・・といった習い方をして、中心に原子をおいて、その周りに電子を配置して、この物質の電子はこんな風に並んでいますと習ったかと思います。右側の図は左の図の主量子数だけの情報を残して、電子の半径方向の位置を視覚的に表したものです。
おそらく右の図は高校で習い、左の図は大学で習うかと思います。高校で習う図は電子の半径方向の位置だけ(主量子数だけ)がわかりますが、大学で習う図は半径方向の位置と、θ、Φ方向、すなわち軌道の形の情報までわかるようになるのです。

3d軌道の縮退解除
電子の軌道をシュレディンガー方程式から求めた今の段階で、もう一度ルビーの赤色について解説したいと思います。ルビーが赤色なのはクロムイオン中のd軌道の縮退が解け、異なる2つのエネルギー状態になり、そのギャップに存在する光の波長の補色が見えるからでした。(詳しくはこちら↓)
[blogcard url=”http://shimaphoto03.com/science/ruby/#shukutai”]
ここでは縮退が解除される理由と、どの軌道のエネルギーが上がったり下がったりするのかを具体的に説明したいと思います。
クロムイオンとそれを取り囲む酸素イオンはこのような形態をとっています。このとき酸素イオンのようなイオンを配位子と呼びます。


クロムはd軌道を持っていて、その軌道は5種類ありました。クロム単体ではその軌道のエネルギーは同じ(縮退)なのですが、配位子がやってくると、エネルギーの高い軌道と低い軌道に分かれます。
以下にエネルギーが高くなる軌道(eg軌道)を示します。


dz2とdx2-y2軌道です。これらの軌道(上図2つ)と他の軌道(下図3つ)の違いを、酸素ークロムの配置図(配位子場の図)と見比べてみてください。



上2つの軌道(dz2とdx2-y2軌道)は酸素イオンに重なるのです。厳密に言えば酸素イオンの電子軌道と重なるのです。酸素の方にも電子が存在しますから、d軌道側の電子と酸素イオンの電子が反発し、(dz2とdx2-y2軌道)のエネルギーが上がるのです。
これが縮退解除の仕組みです。
まとめ
電子軌道を知ることで、その物質の振る舞い(ルビーが赤いなど)を知ることができます。有機化学の世界では物質の電子軌道を参考にしてどんな反応が起こりそうか、どんな物質が安定かを予測したりします。
その時は分子軌道法(MO法)なんかを使ったりします。分子軌道法は「分子の軌道を原子の軌道の線形結合で表す」ということを基本概念としていますから、今回のように原子の軌道を知ることは大切なのです。
※2017年12月追記
分子軌道計算の基礎、単純ヒュッケル法についてまとめました。
[blogcard url=”http://shimaphoto03.com/science/molecular-orbital/”]
私は量子力学を専門としておりませんが、基礎方程式を解いて色々なことを解明し、理解するというプロセスは流体力学などと同じなので、この記事を執筆するのが楽しかったです。(gnuplotの取り扱いでストレスを感じましたが。)今後も色々な現象にチャレンジしてみたいと思います。
スポンサーリンク
 らい・ぶらり
らい・ぶらり


コメントを残す