資料請求番号：TS36 TS41 TS91

一般化した複雑な電気回路や機械力学の微分方程式をラプラス変換で解く

こちら↓の記事でラプラス変換の基礎的な説明と簡単な演習を行いました。

ラプラス変換の基礎と応用～簡単な電気回路・運動方程式を解いてみる～

今回は、ラプラス変換による微分方程式の求解に慣れてきた人のために、より一般化した、すなわち複雑な微分方程式の例題を取り扱っていきたいと思います。

RLC直列回路のステップ応答

こちらの記事ではRL直列回路を取り扱いましたが、今回はコンデンサCも含む、RLC直列回路を取り扱います。回路方程式は以下の通りです。
$$Ri(t)+L\frac{di(t)}{dt}+\frac{1}{C}{\int }_0^{t}i(t^{\prime })d{t}^{\prime }=V_0$$
さらに、今回はステップ関数Θを使用し、ある時刻t=0において、回路のスイッチを入れたとき、その応答はどのようになるか？を計算します。
$$Ri(t)+L\frac{di(t)}{dt}+\frac{1}{C}{\int }_0^{t}i(t^{\prime })d{t}^{\prime }=V_0\mathrm{\Theta }(t)$$
このようなステップや、後ほど取り扱うインパルスに対する過渡応答の解析と言うのはラプラス変換の得意とするところです。

上の式を微分します。ステップ関数は微分するとインパルス関数になります。
$$Ri(t)+L\frac{di(t)}{dt}+\frac{1}{C}{\int }_0^{t}i(t^{\prime })d{t}^{\prime }=V_0\mathrm{\Theta }(t)$$

$$L\frac{d^{2}i(t)}{d{t}^2}+R\frac{di(t)}{dt}+\frac{i(t)}{C}=V_0\delta (t)$$

さらに、両辺をLで割ったこの式をラプラス変換していきます。
$$\frac{d^{2}i(t)}{d{t}^2}+\frac{R}{L}\frac{di(t)}{dt}+\frac{i(t)}{LC}=\frac{V_0}{L}\delta (t)$$

まず、1項目をラプラス変換すると以下のようになります。（※ここで？になった方はこちらをチェック！）
$$\mathcal{L}\left[\frac{d^{2}i(t)}{d{t}^2}\right]=s^2\mathcal{L}[i(t)]–si(0)–\frac{di(0)}{dt}$$

求めるべき関数i(t)のラプラス変換をI(s)とおき、

$$\mathcal{L}[i(t)]=I(s)$$

回路のスイッチを入れる瞬間t=0では電流が流れていないことから

$$i(0)=0\text{and}\frac{di(0)}{dt}=0$$

よって

同様に他の項もラプラス変換すると、以下のような代数方程式が得られます。1. $$\mathcal{L}\left[\frac{d^{2}i(t)}{d{t}^2}\right]=s^{2}I(s)$$

2. $$\mathcal{L}\left[\frac{R}{L}\frac{di(t)}{dt}\right]=\frac{R}{L}sI(s)$$

3. $$\mathcal{L}\left[\frac{i(t)}{LC}\right]=\frac{1}{LC}I(s)$$

4. $$\mathcal{L}[\frac{V_0}{L}\delta (t)]=\frac{V_0}{L}$$

$$s^{2}I(s)+\frac{R}{L}sI(s)+\frac{1}{LC}I(s)=\frac{V_0}{L}$$

代数方程式を解きます。
$$s^{2}I(s)+\frac{R}{L}sI(s)+\frac{1}{LC}I(s)=\frac{V_0}{L}$$

$$(s^2+\frac{R}{L}s+\frac{1}{LC})I(s)=\frac{V_0}{L}$$

$$I(s)=\frac{\frac{V_0}{L}}{s^2+\frac{R}{L}s+\frac{1}{LC}}$$

$$I(s)=\frac{\frac{V_0}{L}}{s^2+Bs+{\omega }_0^2}$$

このとき、
と置きました。

RLC直列回路の過渡応答は

$$b^2={\omega }_0^2–\frac{B^2}{4}=\frac{1}{LC}–\frac{R^2}{4L^2}$$

と置いたとき、b²の値によってその解の形が変化しますので、
b²>0, b²=0, b²<0に場合分けして
ラプラス逆変換を行い、解を求めます。

b²＞0の場合

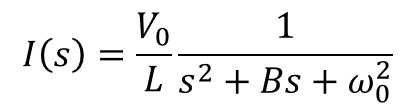
$$I(s)=\frac{\frac{V_0}{L}}{s^2+Bs+{\omega }_0^2}$$

をラプラス逆変換します。変換表

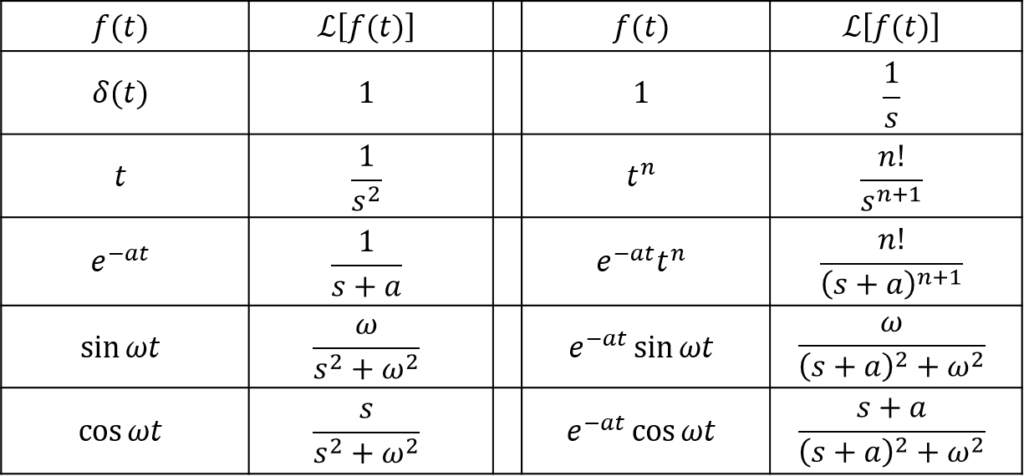
出典：斎藤制海・徐 粒 共著，計測と制御シリーズ　制御工学　－フィートバック制御の考え方ー，第１版第１刷，2003年，pp.19
より、

$$\mathcal{L}[e^{-at}\sin \omega t]=\frac{\omega }{(s+a{)}^2+{\omega }^2}$$

であるから、記号を置き換えて

$$\mathcal{L}[e^{-\frac{B}{2}t}\sin bt]=\frac{b}{{(s+\frac{B}{2})}^2+b^2}=\frac{b}{s^2+Bs+\frac{B^2}{4}+{\omega }_0^2–\frac{B^2}{4}}=\frac{b}{s^2+Bs+{\omega }_0^2}$$

を得ます。

従って、求める電流の時間変化i(t)は

$$I(s)=\frac{V_0}{L}\frac{1}{b}{\mathcal{L}}^{-1}\left[\frac{b}{s^2+Bs+{\omega }_0^2}\right]$$

$$i(t)=\frac{V_0}{L}\frac{1}{b}{e}^{-\frac{B}{2}t}\sin bt$$

となります。

b²＝0の場合

$$b^2={\omega }_0^2–\frac{B^2}{4}=0$$

$${\omega }_0^2=\frac{B^2}{4}$$
より、
代数方程式の解は以下のように変形できます。
$$I(s)=\frac{\frac{V_0}{L}}{s^2+Bs+{\omega }_0^2}$$

$$I(s)=\frac{\frac{V_0}{L}}{s^2+Bs+\frac{B^2}{4}}=\frac{\frac{V_0}{L}}{{(s+\frac{B}{2})}^2}$$
ラプラス変換表から
$$\mathcal{L}[t^n{e}^{-at}]=\frac{n!}{(s+a{)}^{n+1}}$$

$$\mathcal{L}[t{e}^{-at}]=\frac{1}{(s+a{)}^2}$$

$$\mathcal{L}[t{e}^{-\frac{B}{2}t}]=\frac{1}{{(s+\frac{B}{2})}^2}$$

となるので、

ラプラス逆変換を行い、以下の解を得ます。

$$i(t)=\frac{V_0}{L}{\mathcal{L}}^{-1}\left[\frac{1}{{(s+\frac{B}{2})}^2}\right]$$

$$i(t)=\frac{V_0}{L}t{e}^{-\frac{B}{2}t}$$

b²＜0の場合

代数方程式の解を以下のように変形します。
$$I(s)=\frac{\frac{V_0}{L}}{s^2+Bs+{\omega }_0^2}$$

$$=\frac{\frac{V_0}{L}}{s^2+Bs+\frac{B^2}{4}–\left\{{\omega }_0^2–\frac{B^2}{4}\right\}}$$

さらに、

$$b^2={\omega }_0^2–\frac{B^2}{4}$$

と置いているので、

$$I(s)=\frac{\frac{V_0}{L}}{{(s+\frac{B}{2})}^2–(-b^2)}$$

これをラプラス逆変換します。
ラプラス変換表には記載がありませんが、
$$\mathcal{L}[\frac{1}{\omega }{e}^{-at}\sinh \omega t]=\frac{1}{(s+a{)}^2–{\omega }^2}$$

このような公式がありますので、今回のケースに当てはめて考えると

$$\mathcal{L}[\frac{1}{\sqrt{-b^2}}{e}^{-\frac{B}{2}t}\sinh \sqrt{-b^2}t]=\frac{1}{{(s+\frac{B}{2})}^2–(-b^2)}$$

これによりラプラス逆変換を行い、解を得ます。

$$i(t)=\frac{V_0}{L}{\mathcal{L}}^{-1}\left[\frac{1}{{(s+\frac{B}{2})}^2–(-b^2)}\right]$$

$$i(t)=\frac{V_0}{L}\frac{1}{\sqrt{-b^2}}{e}^{-\frac{B}{2}t}\sinh \sqrt{-b^2}t$$

機械力学（バネーダッシュポット系のインパルス応答）

次は、以下の方程式をラプラス変換によって解くことを考えます。
$$\frac{d^{2}x(t)}{d{t}^2}=-{\omega }_0^{2}x–2\gamma \frac{dx}{dt}+\frac{F}{m{\omega }_0}\delta (t)$$

これは、質量mの物体にバネを取り付け、その物体に一瞬だけF/mω₀なる刺激を与えたら物体はどのように運動するか？という問題です。一瞬の刺激ではなく、持続的に力を加えた場合の応答は

$$\frac{d^{2}x}{d{t}^2}=-{\omega }_0^{2}x–2\gamma \frac{dx}{dt}+F_0\cos \omega t$$

で表現でき、この微分方程式を↓こちら↓
のページでルンゲクッタ法により解きました。
[blogcard url=”http://shimaphoto03.com/science/rk-vib/”]

δ(t)をインパルス関数と言い、ある時間t=t₀の時だけ値が∞になって、あとはゼロになる関数です。この関数はラプラス変換をとると1になります。

従って、

$$\frac{d^{2}x(t)}{d{t}^2}=-{\omega }_0^{2}x–2\gamma \frac{dx}{dt}+\frac{F}{m{\omega }_0}\delta (t)$$

として、初期条件

$$x(0)=0,\frac{dx(0)}{dt}=0$$

のもと、それぞれの項をラプラス変換すると

1. $$\mathcal{L}\left[\frac{d^{2}x(t)}{d{t}^2}\right]=s^{2}X(s)$$

2. $$\mathcal{L}[-{\omega }_0^{2}x]=-{\omega }_0^2\mathcal{L}[x(t)]=-{\omega }_0^{2}X(s)$$

3. $$\mathcal{L}[-2\gamma \frac{dx}{dt}]=-2\gamma (s\mathcal{L}[x(t)]–x(0))=-2\gamma sX(s)$$

4. $$\mathcal{L}[\frac{F}{m{\omega }_0}\delta (t)]=\frac{F}{m{\omega }_0}$$

となり、代数方程式
$$s^{2}X(s)=-{\omega }_0^{2}X(s)–2\gamma sX(s)+\frac{F}{m{\omega }_0}$$
を得ます。これを解くと

$$(s^2+{\omega }_0^2+2\gamma s)X(s)=\frac{F}{m{\omega }_0}$$

$$X(s)=\frac{\frac{F}{m{\omega }_0}}{s^2+{\omega }_0^2+2\gamma s}$$

となりますので、これをラプラス逆変換します。

変換表

出典：斎藤制海・徐 粒 共著，計測と制御シリーズ　制御工学　－フィートバック制御の考え方ー，第１版第１刷，2003年，pp.19
より、

$$\mathcal{L}[e^{-at}\sin \omega t]=\frac{\omega }{(s+a{)}^2+{\omega }^2}$$

であるので、これを今回得られた代数方程式に合うよう変形していきます。

$$\mathcal{L}[e^{-\gamma t}\sin {\omega }_{0}t]=\frac{{\omega }_0}{(s+\gamma {)}^2+{\omega }_0^2}$$

$$=\frac{{\omega }_0}{s^2+2\gamma s+{\gamma }^2+{\omega }_0^2}$$
このとき、分母のγ²がが余計になるので、ω₀を√ω₀²–γ²と置き換えて、γ²を消去します。

$$\mathcal{L}[e^{-\gamma t}\sin {\omega }_{0}t]=\frac{{\omega }_0}{(s+\gamma {)}^2+{\omega }_0^2}$$

$$=\frac{{\omega }_0}{s^2+2\gamma s+{\gamma }^2+{\omega }_0^2}$$
↓
$$\mathcal{L}[e^{-\gamma t}\sin \sqrt{{\omega }_0^2–{\gamma }^2}t]=\frac{\sqrt{{\omega }_0^2–{\gamma }^2}}{s^2+2\gamma s+{\gamma }^2+{\omega }_0^2–{\gamma }^2}$$

$$=\frac{\sqrt{{\omega }_0^2–{\gamma }^2}}{s^2+2\gamma s+{\omega }_0^2}$$

これにより、

$$\mathcal{L}[e^{-\gamma t}\sin \sqrt{{\omega }_0^2–{\gamma }^2}t]=\frac{\sqrt{{\omega }_0^2–{\gamma }^2}}{s^2+2\gamma s+{\omega }_0^2}$$

の関係を得られるので代数方程式

$$X(s)=\frac{F}{m{\omega }_0}\cdot \frac{1}{s^2+{\omega }_0^2+2\gamma s}$$

の逆ラプラス変換が可能になります。

$$X(s)=\frac{F}{m{\omega }_0}\cdot \frac{1}{s^2+{\omega }_0^2+2\gamma s}$$

$$x(t)=\frac{F}{m{\omega }_0}{\mathcal{L}}^{-1}\left[\frac{1}{s^2+{\omega }_0^2+2\gamma s}\right]$$

$$x(t)=\frac{F}{m{\omega }_0}\cdot \frac{1}{\sqrt{{\omega }_0^2–{\gamma }^2}}{\mathcal{L}}^{-1}\left[\frac{\sqrt{{\omega }_0^2–{\gamma }^2}}{s^2+2\gamma s+{\omega }_0^2}\right]$$

$$x(t)=\frac{F}{m{\omega }_0}\cdot \frac{1}{\sqrt{{\omega }_0^2–{\gamma }^2}}{e}^{-\gamma t}\sin \sqrt{{\omega }_0^2–{\gamma }^2}t$$

これにより、バネーダッシュポット系の要素に対し、インパルスを与えたときの応答を求めることができました。