CONTENTS

ベイズ統計学の基本となるベイズの定理について解説

ベイズの定理と言うのは「条件付確率」に関する法則です。今回はこの法則を紹介し、具体例な適用事例についてなるべく直感でわかるようにまとめてみたいと思います。

記号の定義

ベイズの定理では、あまり見かけない記号を用いるので、まずは記号の定義からお話しします。
P(A) ：事象Aが起こる確率
例1：目の数が6つのサイコロを振ったとき、1が出る事象をAとすれば、その確率は
P(A) = 1/6
例2：とある疾病にかかった人100人を呼んで、試験検査を行ったところ、99人に陽性反応が出た。よって、疾病にかかった人間に対して陽性が出る事象をBとすれば、その確率は
P(B) = 0.99
P(A|B)：事象Bが発生した下での事象Aが発生する確率
上記は「条件付確率」とか「事後確率」と呼ばれています。
例:事象Aを「ある人間が病気である」、事象Bを「検査結果は陽性」とします。
とあるその辺の人間を何人か呼んで、結果が陽性であると判明したうえで、その人が本当に病気を持っているという事象をP(A|B)で表します。臨床試験の立場で言えばP(A|B)は陽性的中率というわけです。では、この陽性的中率ってどうやって求めればいいの？という問題にあたります。そこで登場するのがベイズの定理です。

ベイズの定理

ベイズの定理によれば、事象Aの確率をP(A)、事象Bの確率をP(B)とし、事象Bが発生した下で、事象Aが発生する確率をP(A|B)とすればP(A|B)は

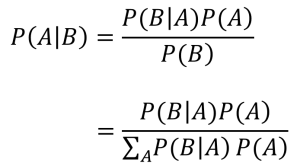（1）

ここで和の記号、Σが出ておりますが、これの言わんとするところは、Aに関する事象の確率をすべて足し上げるという意味です。

臨床試験問題

問題内容

100人に1人がかかると言われている疾病の簡易検査手法が開発されました。この手法を評価するために、疾病にかかった人間100人を呼んで上記の試験をしたところ、99人に陽性反応が出ました。一方で、疾病にかかっていないと分かっている人間100人を呼んで上記の試験をしたところ、10人に陽性反応が出てしまいました。この試験結果をもとに、本手法の評価を行いたいと思います。無作為に集めた人間のうち、陽性であると結果が出たうえで、本当に病気にかかっている確率はいくつでしょう？（陽性的中率の問題）また、陽性であると結果が出たけど、本当は病気じゃない確率はいくつでしょう？（偽陽性の問題）

ベイズの定理の適用

まず、事象Aを「ある人間が病気である」、事象Bを「検査結果は陽性」とします。このとき、問題文と、上述した記号の定義に従えば、陽性的中率はP(A|B)であり、偽陽性率はP(A^C|B)と表せます。（ここでA^Cは余事象をあらわします。つまりP(A^C)はある人間が病気でない確率を表します。）これら2つを求めれば問題が解けたということになります。そしてベイズの定理をこの問題に落とし込めば

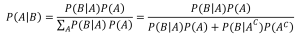　（2）

となります。さきほど、「Aに関する事象をすべて足し上げる」と申しましたが、臨床試験の話ではAに関する事象と言うのは「ある人間が病気である」という事象と「ある人間が病気でない」という事象の２つなので、Σを展開したとき、項が二つになります。

問題文を記号化する

さて、（2）式の記号を、臨床試験問題を例に一つ一つ確認していきましょう。
まずP(A)はある人間が病気である確率です。今は100人に1人がかかる病気について議論しているのでP(A)=0.01です。（※無作為に集めた人という文に注意してください）そして、その余事象の確率はP(A^C)=0.99です。
続いてP(B|A)は事象Aが発生した下での事象Bが発生する確率です。つまり、問題文に書いてある「疾病にかかった人間100人を呼んで上記の試験をしたところ、99人に陽性反応が出ました。」という情報から、「疾病が発生した人間（事象A）の集団に対し、陽性が出た（事象B）のは100人中99人だった。」と読み替えることができるのでP(B|A)＝0.99です。
続いてP(B|A^C)ですが、「疾病にかかっていないと分かっている人間100人を呼んで上記の試験をしたところ、10人に陽性反応が出てしまいました。」と言う情報から
P(B|A^C)=0.10です。

計算する

ベイズの定理に従って、陽性的中率を求めましょう

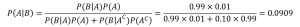
陽性的中率は9.1％ということになります。
次に偽陽性率を求めましょう

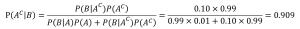
偽陽性率は91%と言うことになります。

結果を考察する

実際に病気になった人100人に検査を施したところ、99人に陽性反応がでたため（※P(B|A)＝0.99）　検査の正確性は高いと言えますが、病気になる確率そのものが低いP(A)=0.01ため、陽性だったけど、そのうち疾病にかかっていない人は91％という、偽陽性の誤診の可能性を孕んでいると言えそうです。

ベイズの定理の使いどころ（まとめ）

定理と言うものは使うと便利だから発明され、有名になって、私たちの目にかかるわけです。ベイズの定理の意義と言うのは、数学的に表現すれば
P(B|A)から P(A|B)がわかるということになります。
つまり、臨床試験問題を例にとれば、事象Aが「ある人間が病気である」、事象Bが「検査結果は陽性」でした。どこ馬の骨かわからん人間を呼んで検査して、陽性がでて、その人間が本当に疾病にかかっている確率と言うものは分かりにくいものです。でも、疾病にかかってると分かっている人間を呼んで検査して陽性になる確率を求めることは簡単です。簡単な試験や実験から、求めることが困難な確率を求めることができるというところにベイズの定理の意義があります。

感想

以下は単なる、しままるの感想です。
ベイズの定理は、私の友人が紹介してくれたものです。その友人と私とでは専攻の内容が全く異なり、得意とする学問は異なります。ところが、この定理はラプラスが本格的に使用・普及させたという歴史があるそうです。ラプラスと言えば、微分方程式を解くためのラプラス変換やベクトル解析でお目にかかるラプラシアン演算子で有名です。また、定常の熱・物質・運動量の拡散の問題はラプラス方程式です。これは私の専門分野です。専攻の内容が異なるのに、同じ先人が定理や法則を発見していたんだ～という驚きと言うか、感動というか、そんな所感を抱きました。
また、ラプラスと検索するとポケモンのラプラスばかりの情報が出てきて、1ページ目にはピエール・シモン＝ラプラス氏の情報や業績が出てこないという、科学好きとしては「う～ん」という感じですが、まぁ、ポケモンのラプラスは可愛いから良しとしましょう！