CONTENTS

回転の数式と現象のイメージを結ぶ

流体力学、電磁力学には「∇×」といったベクトル解析の演算子がたくさん出てきます。このとき、ベクトル解析の内容をしっかり理解していないと、もうその時点でその分野の勉強が進まなくなってしまいます。ここでは、ベクトル解析の「回転」と呼ばれる演算子をテーマに、回転の定義（数式）と実際の現象のイメージを結び付け、頭の中をスッキリさせた状態にしていただくことが目的です。

回転の定義

ベクトル解析の基本を説明したページ（こちら）で回転について

「回転」の定義は以下の通りです。

あるベクトル変数A=(A_x, A_y, A_z)があったとき、Aの回転∇×Aは

で表される。

と説明しました。このページではこの定義の物理的イメージについて書いてみたいと思います。

回転のイメージ

右ねじの法則

回転は「ローテーション」とも呼ばれていて、「∇×」とか「rot」とか「curl」といった記号で表されます。右ねじの法則というものを知っていますか？ねじは「の」の字に回すと材料の奥へ入っていきますよね。回転という物理的な力を与える（トルクを与える）ことでねじは材料に対して下へ下へ力を与えていきました。そして、強く回転させるほど強く下に力が加わりました。

回してそれに対して垂直な方向に回した力に対応した力が働いている。この現象を数式にしようとしてできたのが「回転」です。

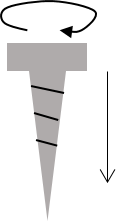　回転のイメージ

回転を数式で表す

ねじを回せば下向きに力が働きます。棒に電流を流すと棒に対して垂直な平面に磁場が発生します。流体の流れが激しくなれば渦が発生し、周囲に影響を及ぼします。

こういった現象を解析するには「回転」詳しく言えば「回転の強さ」というものを数式で表現しなければいけません。では回転の強さって何なんでしょうね？今回は「川に流される桜の花びらの運動」を例に「回転の強さって何だろう」という漠然とした疑問に挑戦したいと思います。

川に流される桜の花びら

川に流される桜を撮影してみました。

動画の桜は右方向に流されながら、ちょっと左を向いて、右にクルッと回りましたね。この現象を細かく見ていきます。

回るということは桜には並進運動（形を保ったまま運動）するための一様な流れ（図１、図２の流れ）以外にも何らかの流れが働いていると言えるでしょう。

つまり、図1や図2の流れ以外にも、違う流れ（一様でない流れ）があるから桜は回る。

では、こんな感じの流れを考えてみましょう。

桜の周りをクルクル回る流れ。これを方向の成分で分解すると

u_xは左図のように、u_yは右図のように分解できます。

u_xの後ろに縦棒のようなものがあって、その下にyと書かれていますが、これは位置yにおけるu_xの大きさという意味です。

回転というのは、このように物体の位置によって速度が異なることによって生まれます。（※図1や図2の場合は物体のどこでも同じ速度でした。だから並進運動になるのです。）

回転を数式にする

色々な位置における速度を合計して、物体にかかる正味の流体の速度を出します。これが回転の強さになります。また、図4では物体（今回は桜の花びら）のy方向の長さ、図5では物体のx方向の長さ（物体依存のパラメータ）によってに回転のしやすさが変わってくる（正方形の物体と細長い長方形の物体とでは回転のしやすさが違う）ので、単位長さ当たりの正味の流体の速度を出します。

図4の場合

（1-1）

図5の場合

(1-2)

回転に寄与する速度は(1-1)と(1-2)の合計ですから

（1-3）

これはまさに∇×uのk方向成分ですね。この数値が大きくなるということは図3の速度が上がり、（1-1）や（1-2）で計算した正味の流体の速度が大きくなることを示します。すなわち、xy平面における回転が強いという意味になります。またこの数値が０であれば、その流体の流れに回転はないとみなすことができます。これによって、回転の強さを数式で表現することができるようになりました。これでねじが下方向に与える力の強さや電流によって発生する磁場の強さを表現できるようになります。