資料請求番号:TS92 スポンサーリンク
マクスウェル方程式と現象のイメージを結ぶ
マクスウェル方程式は「電磁気現象を表現する4つの基礎式」です。この4つの基礎式は色々と難しい記号が使われていて初学者にはなかなか理解が難しいものだと思います。
この記事では4つの基礎式を紹介し、それぞれがどんな現象を表しているのか、なるべく直感的なイメージを浮かべられるように説明することを目的とします。イメージ優先ですので厳密な部分で間違いがあるかもしれませんがご了承ください。
4つの基礎式
マクスウェルの方程式は以下の4つの式で成り立ちます。
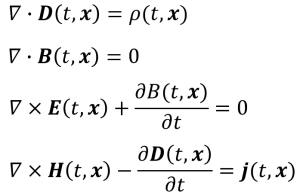
・・・と言われてもなぁという感じですよね。わけのわかんない記号がいっぱいあったり、太字だったり・・。
でも、この方程式で電気が流れる、磁石がくっつくことは然ることながら、電話ができる理由や虹ができる理由、葉っぱが緑色である理由など、電磁波にまつわる現象を説明できるものすごい式なんです。
これだけあらゆる現象をたった数個の数式で表現するには、これだけ複雑な式を使わなければならない。ということなんです。
ここでは上記4つの方程式を(厳密な理解はさておいて)なんとなく理解することを目標にします。
変数の説明
まず、方程式に使われている変数(アルファベット)の意味を紹介します。
・D(電束密度)
単位: C/m2 (クーロン パー 平米)または A・s・m-2
意味:単位面積当たりの電束の数
クラス:ベクトル(基本的にベクトルは太字で表記します。)
(電束密度は方向の情報を併せ持っています。だからベクトルです。)
(電束というのは理科で習った電気力線の束のようなものを考えてください。
これがいっぱいあるほど強い電流が流れているというイメージです。)
・B(磁束密度)
単位:T(テスラ) または Wb/m2 (ウェーバー パー 平米)または kg・s-2・A-1
意味:単位面積当たりの磁束の数
クラス:ベクトル
・E(電場)
単位:V/m(ボルト パー メートル)またはkg・m・s-3・A-1
意味:電場Eの中に電荷qを置いたとき、F = qEの力が生じる。
(こんな感じで、別のものが作用したとき、初めて物理的な変化が起こる「場」について表現する物理量があります。私たちの身近な例でいえば重力場です。質量1㎏のリンゴを高さ10mの位置から落とせばリンゴは落下します。これは重力場gにおいて、質量mが作用したので、F=mgの力が働いたと解釈できます。)
クラス:ベクトル
・H(磁場)
単位:N/Wb(ニュートン パー ウェーバー) または A/m
意味:電場Hの中に磁荷qを置いたとき、F = qHの力が生じる。
(ただし、磁荷というものは架空のものであり、N極の磁荷が対象であれば、S極は無限遠に存在すると仮定している。)
クラス:ベクトル
・j(電流密度)
単位:A/m2、C・s-1・m-2
意味:単位時間、単位面積あたりに流れる電気量(クーロン)
クラス:ベクトル
発散、回転
これまで、アルファベットについて説明してきたので、次は謎の記号、∇について見ていきましょう。
発散
発散は「ダイバージェンス」とも呼ばれていて、「∇・」とか「div」といった記号で表されます。ホースから水を撒いたとき、水の中にインクを垂らしたとき、水やインクは四方八方に散らばっていきますよね。(あれ?と思った人は重力や水圧がない状態を想像してください。)基本的に物理量(濃度とか速度とか)というものは四方八方に散らばる方向へ移動します。これを数学的に表したのが「発散」です。イメージ図を描くとこんな感じです。Dという物理量が四方八方に散らばっています。これを数学的に表したのが発散です。

回転
回転は「ローテーション」とも呼ばれていて、「∇×」とか「rot」といった記号で表されます。右ねじの法則というものを知っていますか?ねじは「の」の字に回すと材料の奥へ入っていきますよね。回転という物理的な力を与えることでねじは材料に対して下へ下へ力を与えていきました。
回しているのにそれに対して垂直な方向に力が働いている。このなんとも表現しがたい現象を数式にしてできたのが「回転」です。
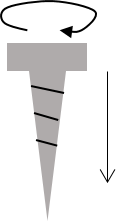 回転のイメージ
回転のイメージ
4つの方程式の意味
さて、いよいよ本題です。4つの方程式を直感的に理解してみましょう。
マクスウェル-ガウスの式
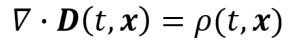
電荷があると、四方八方に散らばる電場Dが発生するよ(電場Dが発散するよ)。
という意味の式です。これを図式化すればこんな感じ。

電荷密度ρ[C/m3]をある場所に置くと、その周りに電場Dができます。その電場Dは四方八方に飛び散る方向を向いたベクトルです。(Dは発散しています)
tというのは時間、xは座標を表します。xが太字なのはベクトルだからで、しっかり記述するとx = (x, y, z)です。
磁場保存の式
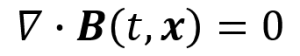
磁荷があっても四方八方に散らばらないよ(発散しないよ)。
という意味の式です。電荷とは違い、磁荷は必ず対をなします。N極だけ、S極だけの磁石など、存在しないのです。そしたら磁力線はどうなるかというと

こうなります。どこにも発散しないのです。だから磁束密度の発散はゼロなのです。
ファラデー・マクスウェルの式
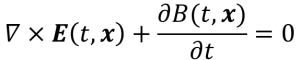
磁束密度を変化させると、その周りに電流が流れるよ。
という意味の式です。
∂は偏微分記号です。微分というものは微小変化量を表すものですよね。∂B/∂tは磁束密度の変化量です。磁束密度が変化すればEの回転ができると式は教えてくれています。図に表すとこんな感じです。
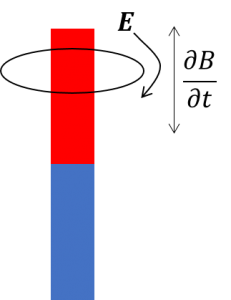
コイルの周りで棒磁石を抜き差しすると電流が生まれるという実験をしたことはありませんか?ファラデーの電磁誘導の法則です。棒磁石を抜き差しするという行為はBの数に時間変化を与えていることに相当します。コイルの周りでBを増やしたり減らしたりすることでEが生まれ、電気が流れるのです。
アンペール・マクスウェルの式
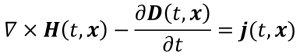
電流jが流れたり、電場が変化したりすると、その周りに磁場が発生するよ。
という意味の式です。
ちょうど、先ほどのファラデー・マクスウェルの式の反対版ですね。電場の変化によっても磁場が生まれるし、磁場の変化によっても電場が生まれるのです。
理科の授業でこんな実験をしたことはありますか?板に砂鉄を撒いて、棒に電気を流すと、砂鉄は輪っかを作ります。これは電流jが流れたことで円盤状の磁場∇×Hが発生したことを表しています。

マクスウェルの方程式 まとめ
最後にもう一回マクスウェルの方程式を示します。
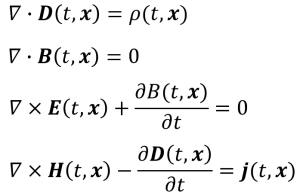
そして、それぞれの意味は
・電荷密度ρがあると電場が発散する(湧いて出てくる)
・磁場は発散しない
・磁束密度を変化させると電流が生まれる
・電流によって磁場が発生する
ということになります。こうしてみてみるとごくごく当たり前のことを言っているような気がしますが、この自然界の当たり前を数式で表現することが難しいことですし、面白いことでもあります。この記事を読んでマクスウェルの方程式がなんとなくわかった方がいれば幸いです。
 らい・ぶらり
らい・ぶらり


コメントを残す