資料請求番号:TS39
スポンサーリンクラプラシアンの極座標変換の式変形を詳細に追う
大学数学で偏微分を勉強すると、ラプラシアンの極座標変換を行え。といった問題が試験などで出題されることがあると思います。
数検1級の問題でも
出典:日本数学検定協会
といった問題が出題されました。
ラプラシアンといった、演算子の座標変換は慣れないうちは少し苦労します。x, y, r, θと変数が色々出てきて、何を何で微分すればいいのか、頭が混乱することもあるでしょう。
ただし、慣れてしまえば、かなり簡単な問題であり、点数稼ぎのための良い問題になります。
本記事では、2次元の極座標表示のラプラシアンを導出します。導出の際は、細かな式変形も逃さず記して、なるべくゆっくり、詳細に進めていきたいと思います。
ラプラシアンの極座標変換にはベクトル解析を使う方法などありますが、今回は大学入りたての数学のレベルの人が理解できるように、地道に導出を進めていきます。
問題のゴール

確かこの問題、大学1年生の時にやった覚えがあるけど・・・。今はもう忘れちゃったな~。
そもそも、ラプラシアンを極座標で表したときの形を求めなさいと言われても、正直、答えの形がよく分からなくて困ったような気がする。

要は座標変換なんだよな。高校生の時に直交座標表示された方程式を出されて、これの極方程式を求めて、概形を書いたり最大値、最小値を求めたりとかしなかったか?

うん。やったね・・・。

極方程式の形にはもはやxとyがなくて、rとθだけの式になっているよな。
x = rcosθとy = rsinθを上手く使って、与えられた方程式からx,yを消していき、r,θだけの式にする作業をやったんだよな。

そうそう。この余計なところにあるxをどう処理しようかな~なんて悩んだ事あるな~。

今回はこれと同じことをラプラシアン演算子を対象にやるんだ。

この直交座標のラプラシアンをr,θだけの式にするってこと?

そうだ。解答のイメージとしてはこんな感じだ。
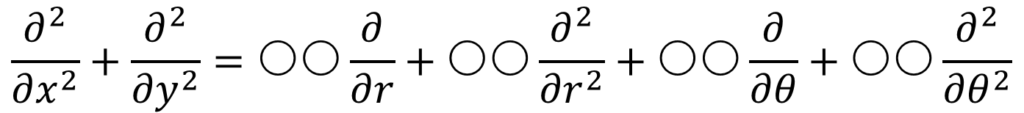

〇〇のなかには、rとθの式が入る。地道にx,yを消していった結果、この〇〇の中にrとθで表される項が出てくる。その項を求めていくぞ。
1階偏導関数の極座標化
チェイン・ルール

2変数関数の合成関数の微分にはチェイン・ルールという、定理がある。
x,yが全微分可能で、x,yがともにr,θの関数で偏微分可能ならば
 ・・・①
・・・①

今回の場合、x = rcosθ、y = rsinθなので、ちゃんとx,yはr,θの関数になっている。もちろん偏微分も可能だ。
∂/∂xの極座標化

この赤い四角と青い四角は何?

最終目標はr,θだけの式にすることだったよな?赤や青で囲った部分というのはxの偏微分が出ているから邪魔だ。式変形してあげなければならない。

rをxで偏微分しなきゃいけないということか・・・。rはxの関数だからもちろん偏微分可能・・・だけど、rの形のままじゃ計算できないから、
rをxとyの式にしてあげないといけないわね。

そうそう。問題に与えられているx = rcosθ、y = rsinθから、rは簡単にxとyの式にすることができるよな。ついでに、θもxとyの式にできるよな。
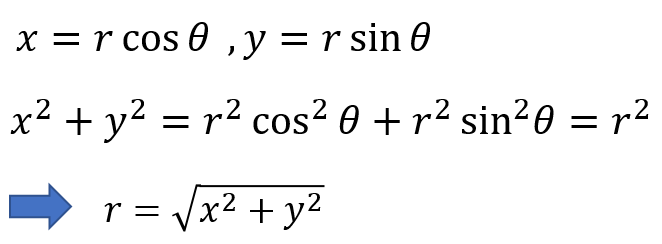
![]()

その上で、赤四角で囲った部分を計算してみるぞ。微分の基本的な計算だ。
この計算の流れがちょっと理解しづらい場合は、高校数学の合成関数の微分のところを復習しよう。
 ・・・②
・・・②

同様に青四角の部分もこんな感じに求められる。Tan-1θの微分は1/(1+θ2)だったな。
 ・・・③
・・・③

そしたら、さっきのチェイン・ルールで出てきた式①は以下のように変形される。
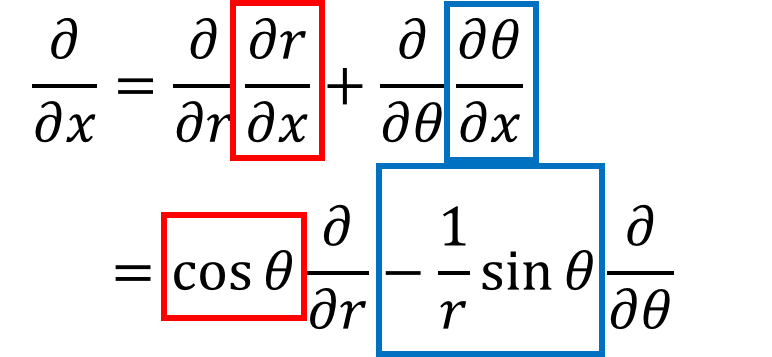 ・・・④
・・・④

あっ!xとyが完全に消えて、rとθだけの式になったね!

そうなんだ。こういう作業を地道に続けていく。
∂/∂yの極座標化

さっきと同じ手順で∂/∂yも極座標化するぞ。
 ・・・⑤
・・・⑤
 ・・・⑥
・・・⑥
 ・・・⑦
・・・⑦
⑤式に⑥、⑦式を代入して
 ・・・⑧
・・・⑧

次は簡単に計算できた!

まぁ、基本的にxとyが入れ替わって同じことをするだけだからな。
2階偏導関数の極座標化
∂2/∂x2の極座標化

今回、俺らが求めなくちゃいけないのは、2階偏導関数だ。先ほど求めた1階偏導関数をもう一回偏微分する。カッコの中はさっき求めた∂/∂xで④式だ。
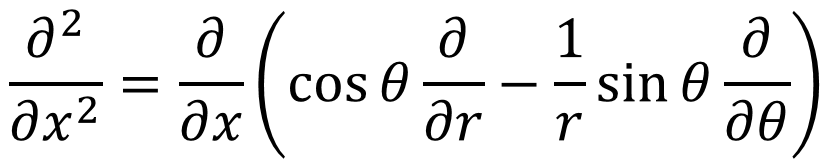 ・・・⑨
・・・⑨

今回、気を付けなくちゃいけないのは、カッコの中をxで偏微分する計算を行うことになる。ただの掛け算じゃなくて微分しているということを意識しないといけない。
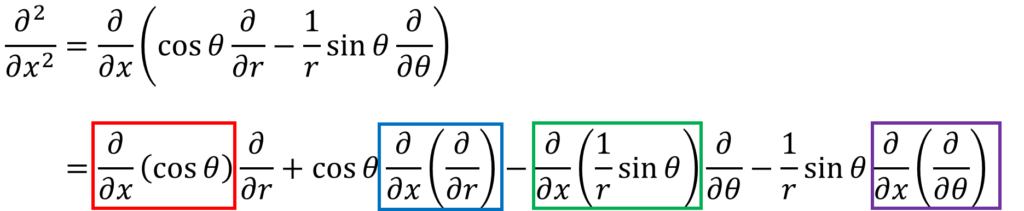 ・・・⑩
・・・⑩

あ、これ合成関数の微分の形になっているのね。(fg)’=f’g+fg’の形。

そうなんだ。ただ単に各項に∂/∂xを付けるわけじゃないんだ。

この計算で、赤、青、緑、紫の四角で示した部分はxが入り混じってるな。再びxを消していくという作業をするぞ。
 ・・・⑪
・・・⑪
 ・・・⑫
・・・⑫

青四角の部分だが∂/∂xが出てきているので、チェイン・ルール(①式)を使う。その時に∂r/∂xやら∂θ/∂xが出てきているが、これらは1階偏導関数を求めたときに既に計算しているよな。②式と③式だ。今回はその計算は省略するぜ
 ・・・⑬
・・・⑬
 ・・・⑭
・・・⑭

よし。これで∂2/∂x2を求める材料がそろったな。⑩式に⑪~⑭式を代入していくぞ。
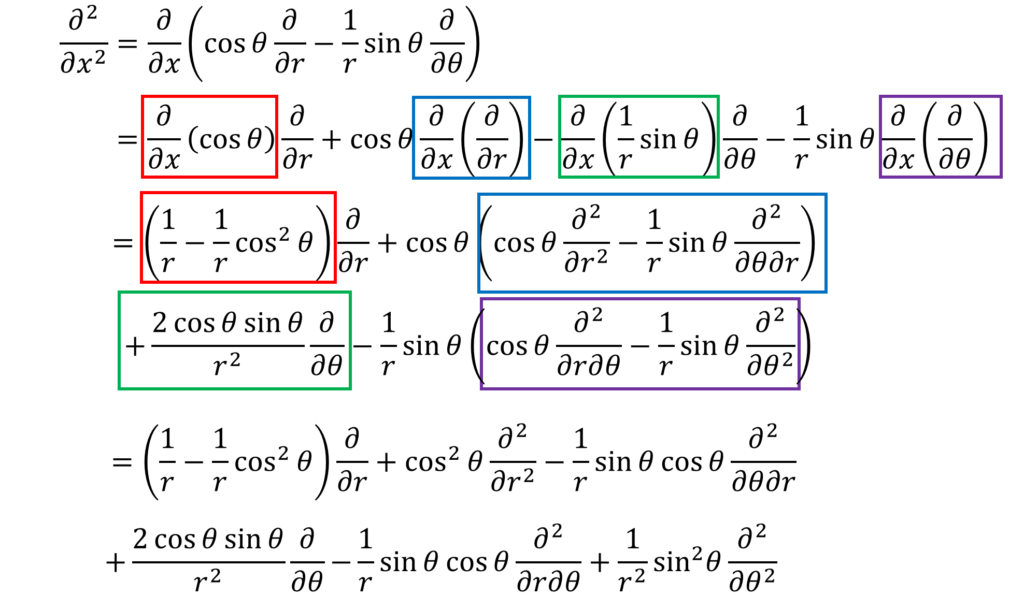 ・・・⑮
・・・⑮

うあっ・・・ちょっと複雑になってきたね。

単に赤、青、緑、紫の部分を式変形してrとθだけの式にして、代入しているだけだ。ちょっと長い式だが、x,yは消え去って、r,θだけになっているのがわかるだろう?

そうね。一応問題としてはこれでOKなのかしら?
∂2/∂y2の極座標化

あと、∂2/∂y2
のときと同じ要領でやっていくぜ
 ・・・⑯
・・・⑯
 ・・・⑰
・・・⑰
 ・・・⑱
・・・⑱
 ・・・⑲
・・・⑲
 ・・・・⑳
・・・・⑳
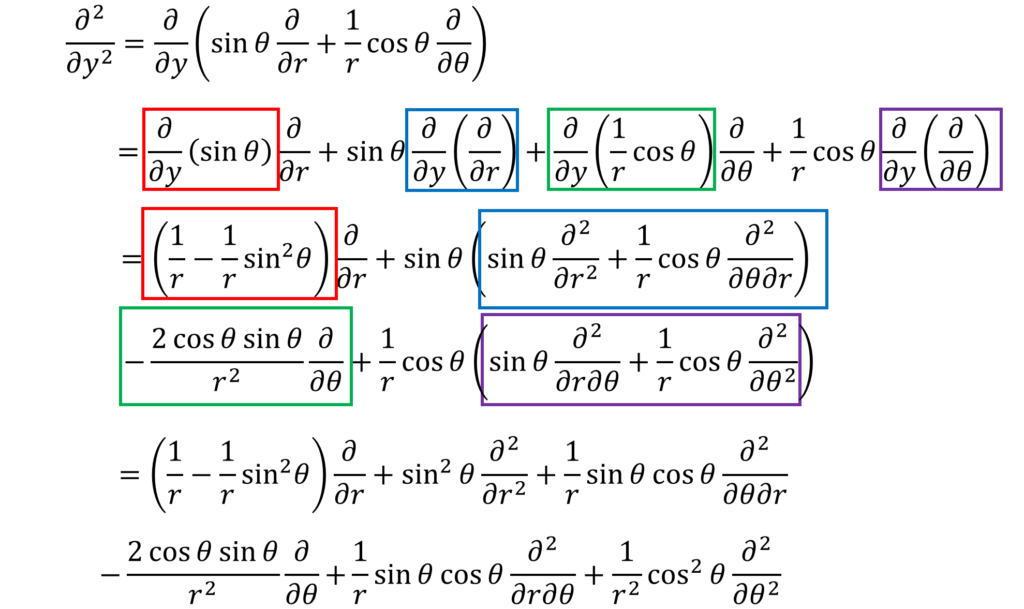 ・・・㉑
・・・㉑

これで∂2/∂x2と∂2/∂y2がそろったのね!これらを足し合わせれば、終わりだね!

・・・でも足し合わせるのめんどくさそう・・。

こういう時は、偏微分演算子の種類ごとに分けて足し合わせていけばいいんじゃないか?∂2/∂x2にも∂2/∂y2にも同じ偏微分演算子があるわけだし。⑮式と㉑式を参照するぜ。
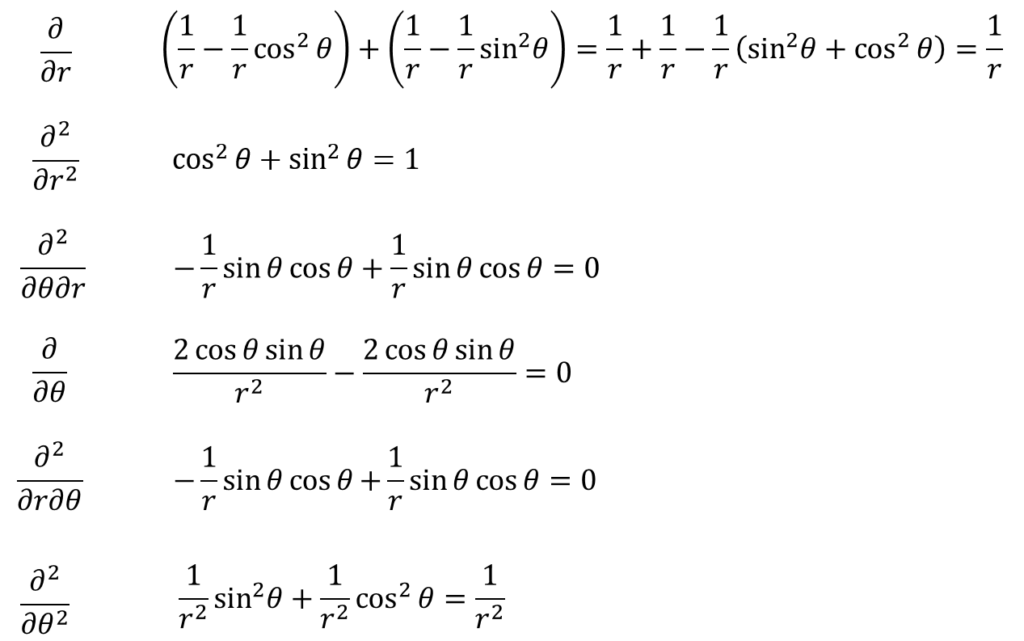 ・・・㉒
・・・㉒

・・・あ、スゴイ!足し合わせたら1になったり、0になったりでかなり簡単になった!
こういうの気持ちいいよね!!

これで各偏微分演算子の項が分かるようになったな。これでラプラシアンの極座標表示は完了だ。
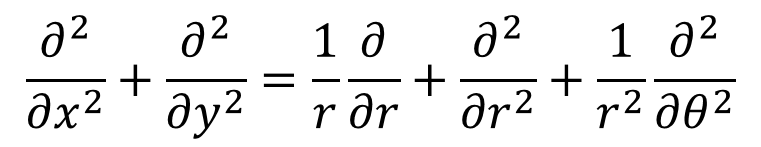 ・・・㉓
・・・㉓
まとめ
今回は、ラプラシアンの極座標表示にするための式変形を詳細に解説しました。ポイントは以下の通り
・高校生の時にやっていた極方程式をもとめるやり方を思い出す。
・x,yを式から徹底的に追い出す。そのために、式変形を行う
・偏微分とただの掛け算とを混同しない
ぜひ、この計算を何回かやってみて、慣れて解析学の単位を獲得してください!
ラプラシアンの極座標変換を応用して、富士山の標高を求めるという問題についても解説しています。
[blogcard url=”http://shimaphoto03.com/science/suuken-fuji/”]
 らい・ぶらり
らい・ぶらり



コメントを残す