資料請求番号:TS42

凧に人が乗るなんて漫画の忍者みたいなことはできるか?
明けましておめでとうございます。年始なのでお正月にちなんだ物理をやってみようと思いまして
凧に人が乗って空を飛ぶことは可能か?
という問題を解いてみました。
本記事では、凧が揚がる原理と、原理に基づいた計算から、仮に凧に人が乗って空を飛ぶのに必要な「凧の面積」と「凧に吹きかける風速」を求めてみました。
そして人間凧の実現可能性について考えてみました。
結果だけ知りたい!という方は「まとめ」部分のみお読みください。
凧揚げを普通に楽しみたい!という方はこちら!凧揚げの方法とコツをまとめております。
[blogcard url=”http://shimaphoto03.com/science/kite/”]
凧が揚がる原理
愛知県豊橋市 シママの実家
この日、シママとディープルは浜松の凧場に行って凧揚げをしてきました。

今日は楽しかったよ!シママ、ありがとう!

いえいえ。ワタシも楽しかったよ!

ところで凧ってさ。忍者みたいに人を載せて飛ぶことってできるのかな?

えー。出来ないんじゃない?重すぎるもん。

・・・・・。

・・・・・。

・・・・・。

・・・・・(え、何?この沈黙は。これって、ストークみたいにもっと論理的に話さないと話進まないヤツ・・・?)

凧にかかる揚力を計算できないとわからないよね。

ま、まぁ確かにそうね。よ、揚力って、どうやって計算するのかしら・・・。ちょっとネットで調べてみようかしら。
・・・・

あった!・・・なるほどね~。

ねぇ、ディープル。こんな論文がネットにあったんだけどね、これを参考にすれば
人が凧に乗って空を飛べるのか?っていう疑問に答えられそうだよ。
ユーザインタラクティブ凧シミュレーションシステムの開発
岡本太一(静岡大学大学院)、藤澤誠(奈良先端科学技術大学院大学)、三浦憲二郎(奈良先端科学技術大学院大学)

・・・これは?

これね!面白いの!凧揚げゲームを作ろうということで、物理を使って凧の動きをコンピュータ上で再現しようっていう趣旨の論文なのよ。
(日本語でよかった~。あとこれ、ファーストオーサーが静岡大学じゃない。浜松まつりとなにか関係があるのかしら?)

なんか、映画とかゲームとかにリアルな水とか物体の動きを再現するのに物理学が使われているって聞いたことあるけど、これもそうなのかな?

うん!そう!こうやって物理モデル化することで、コンピュータが分かる言葉、つまりプログラミングをすることができるようになるのよ。
それでね。さっき浜松の凧場で話した通り、風上に向かって凧を飛ばすと、凧には揚力と抗力が働いて、揚力のお陰で凧は飛べるのよね。
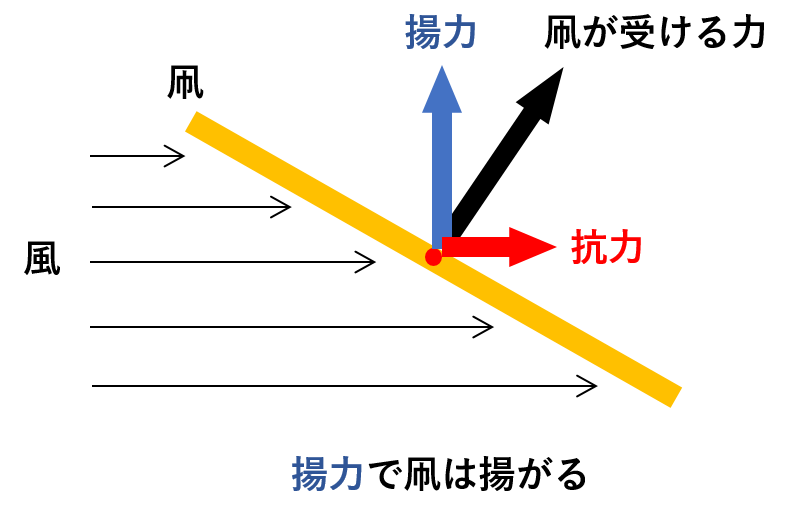

それで、この論文によると、この揚力は以下の式で計算されるんだって。

出典:ユーザインタラクティブ凧シミュレーションシステムの開発

太字がベクトルでこの掛け算マークは外積?

あら、よく知ってるじゃない!

ストークに教えてもらったんだ。

あ~なるほど。ストークにね。
揚力の計算

出典:ユーザインタラクティブ凧シミュレーションシステムの開発

でも、揚力係数とか投影面積とか法線ベクトルって言うのがよくわからないんだ。

うん。一個一個説明してくね。
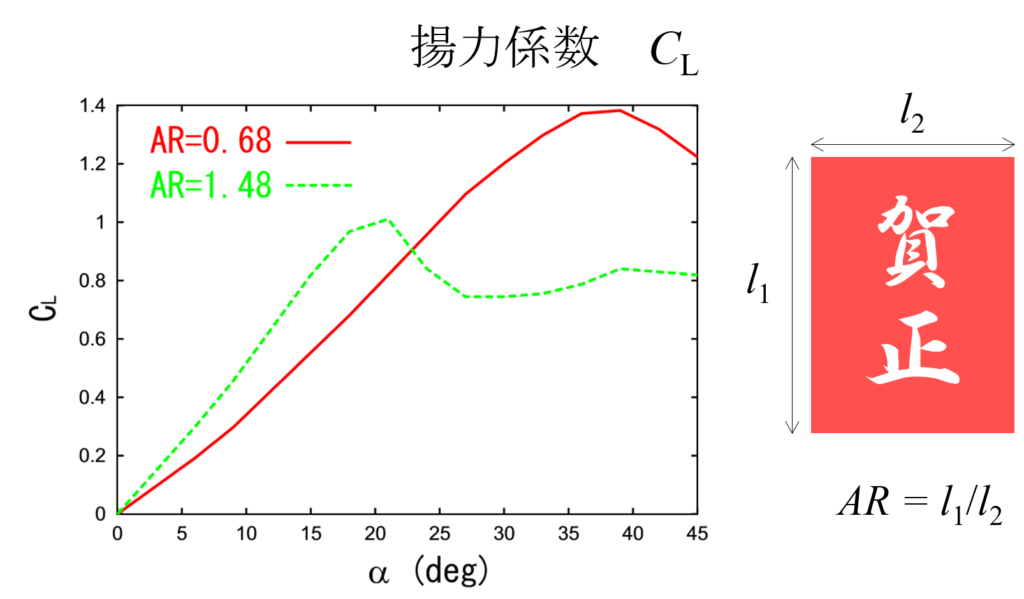
揚力係数

この揚力係数って言うのは地面に対する凧の角度、これを迎角っていうんだけど、迎角によって変わるのよ。あと凧の形によっても変わるみたい。それをアスペクト比0.68の凧と1.48の凧で実験したみたい。
アスペクト比1.48が縦長で0.68が横長。人が乗るってことを想定するなら、縦長(アスペクト比1.48)で計算したほうがいいんじゃないかしら?

揚力係数には、この論文のデータを使うの?

うん。そうだよ。過去の論文を引用して計算なり実験なり、新しい問題にチャレンジして、また論文を出すって言うのが研究者の仕事。
今回の問題は「凧に人を載せて飛ばせることができるか」っていう問題よね。

そうなんだ~。
出典:ユーザインタラクティブ凧シミュレーションシステムの開発
投影面積

投影面積って言うのは、ナナメに傾いた凧に対して光を当てたときにできる影の面積のことを言ってるのよ。
これは「どれだけ風の影響をうけているか」の指標なの。

地面に対して水平な凧って言うのは投影面積ゼロで、風の影響を受けない。逆に地面に対して垂直にすると投影面積は最大になって凧そのものの面積になる。この時、風の影響を強く受けるんだね。

そうそう。(理解が早すぎて追い越されそう・・・。)


zx平面上に凧がθだけ傾いているとすると、x軸の遠方にできる影の高さはl1sinθよね。


うん。y方向の凧の長さは凧の幅l2を表しているから、x軸を90°回転させてyz平面上に映る凧の影を見ると、投影面積はS = l2l1sinθってことがわかるね!

そうね。(まさか正月休みの帰省中にsinだcosだ言うなんて思いもしなかった・・・。)
凧の法線ベクトル

法線ベクトルっていうのは、凧に対して垂直なベクトルのこと。


地面に対して角度θだけ傾いた凧の法線ベクトルって言うのは、z軸方向はcosθ、x軸方向はsinθになるの。そして、この凧はy軸に対して平行だからy成分はゼロ。

なるほど~。これで揚力を求めるのに必要な情報はそろったね!

うん。あとは、迎角ごとに揚力を計算していって、一番揚力が出る角度を求めて、その角度で凧に人が乗るかどうか計算してみよう!
式変形と計算

これまで出してきた情報を元に、投影面積Sや外積部分を計算するとこんな感じになる。


これでExcel使って、角度ごとの揚力を計算するの。

揚力係数はどうするの?論文から値を定規で読み取るの?

ううん。画像化されたグラフを読み取ってデータとして起こしてくれるツールがあるからそれを使うのよ。

へぇ~便利だね~。

これで、諸々の条件を入れて揚力を求めるとこんな感じになる。
条件:
空気の密度:1.247 m/s(外気温10℃)
凧の寸法:高さ(l1) 2.66 m
幅(l2) 1.8 m
気流と凧の相対速度≒風速:x方向に1m/s
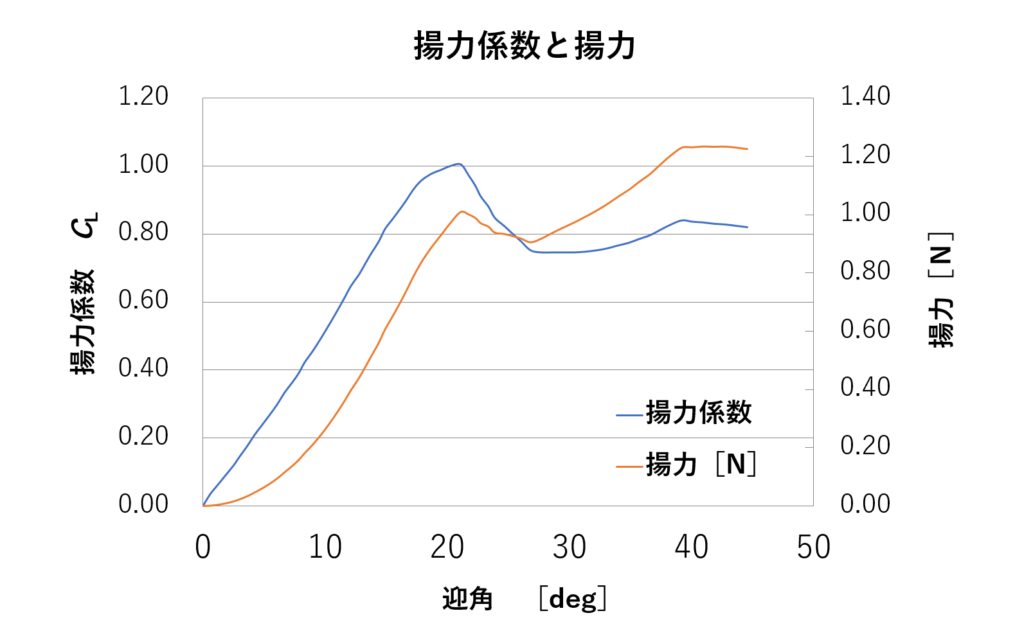

ね?凧が揚がったら、30~40°になるくらいに制御するって言うのもあながち間違ってはいないでしょ?

うん。ホントだ!すごいね!シママ!

ん?まぁ、いや・・・まぁね。

それでね。計算上、最も揚力の出る凧の迎角は40.1°なんだけど、その角度でも凧にかかる揚力は1.2Nくらいなのよ。

凧に乗る人にかかる重力は・・・。乗る人が男の忍者だとして体重60kgに重力加速度がかかるから・・・
600N弱の重力がかかるんだね。これに打ち勝つほどの揚力が必要になるんだ・・・。
人は凧に乗ることができるか?
風速1m/sのとき、必要な面積
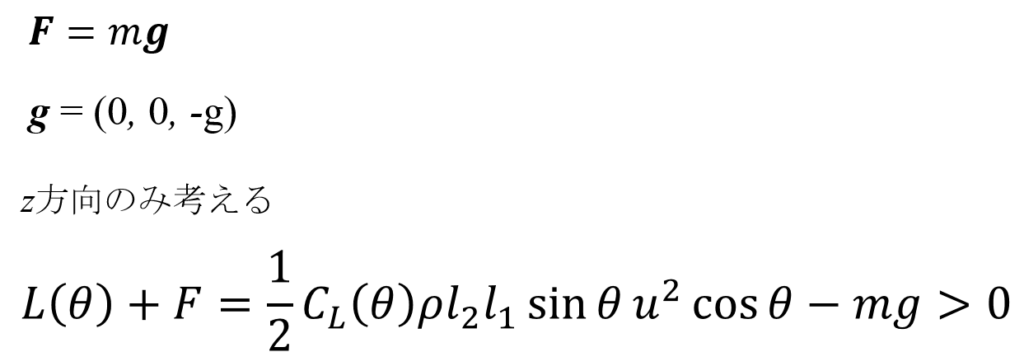

うん。つまりこの式が成立しないと、凧に人を載せて飛ばすことはできないってことになるわね。

今回、一番揚力のかかるθ=40.1°で計算してみるとしても、かなりの面積あるいは風速が要りそうだね。

うん。じゃあ、計算してみようか。
・・・・・

なるほど。

何かわかったの?

こりゃ無理だわ(笑)

やっぱり?

うん。だって、アスペクト比を維持するようにl2を操作変数としてL+Fがゼロになるようなl2を求めたんだけどね、そしたら39.3mだって。つまり、風速1m/sならば、58.2m×39.3mの巨大凧が必要ってことになるのよ。

お・・・大きい。

しかもこれだけ大きいと材質もしっかりしてて、骨組みもしっかりしていないといけないでしょ?計算にない重さがどんどん出てきちゃうのよ。

余計無理になるんだね。

うん。しかも、一番揚力が働いてこの結果だからね~。
縦2.7m、横1.8mの寸法で必要な風速

次は人が乗れそうな大きさで常識的な大きさの凧の寸法であったとして、飛ばすのに必要な風速を計算してみるね。

そしたら?
・・・・

風速21.8m/s

・・・・暴風だね。これじゃあ、色んなもの飛んできて乗ってる人危ないし、今の季節寒そう。

確かにね。

それに、これだけ風が強いと凧の後ろに大きな渦が出来るせいで安定して飛ばすことができなくなるのよ。

確かに。しかも暴風の気象になると一様に21.8m/sの風が吹くことなんてなくて、y方向にもz方向にも吹くだろうから、もうメチャクチャになりそうだね。

う~ん。

やっぱムリだったね!

うん。
まとめ
今回の記事では凧が空を飛ぶ原理と、その原理に基づいた揚力の計算を行い、60kgの人間が凧に乗って空を飛ぶことができるのかを検証してみました。
検証の結果
①風速1m/sの風が吹いている場合、凧の大きさは58.2m×39.3mでなければならない
②凧の大きさを2.7m×1.8mとした場合、風速21.9m/sの風が必要
ということが分かりました。さらにこの計算結果は最適な迎角(地面と凧の角度)が確保された状態における最低限の凧の大きさ、風速です。実際にはさらに大きな凧、大きな風速が必要になるでしょう。
また、①について、凧を大きくすればするほど、凧に使う素材はしっかりとしたものでなければならないうえ、骨組みもしっかりと組まなければなりません。その場合、凧にかかる荷重が大きくなっていくので、さらに現実性がなくなります。
②については一様に風速21.9m/sの風が吹くことは自然現象上あまりなく、それだけの風速がでるような気候ではあらゆる方向へ風が吹いてきます。
したがって揚力ベクトルもメチャクチャな方向になるでしょう。また、風速が大きいと凧の周辺で無数の空気の渦が発達し、これも凧の安定性を落とす要因となります。
以上より、人が凧にのって飛ぶことは、かなり難しいのではないでしょうか。
というのが私の意見です。
 らい・ぶらり
らい・ぶらり

平面凧では不可能ですが、
立体凧を垂直に組み合わせることで、
空は飛べます。
忍者ではなくて、
近代西洋人が実現化しています。