資料請求番号:TS39
スポンサーリンク博士の愛した数式「オイラーの公式」を導出する
オイラーの公式を表現した国語
小川洋子さんの小説、博士の愛した数式には、このような文章があります。
果ての果てまで循環する数と、決して正体を見せない虚ろな数が簡潔な軌跡を描き、一点に着地する。どこにも円は登場しないのに、予期せぬ宙からπがeの元に舞い下り恥ずかしがり屋のiと握手する。彼らは身を寄せ合い、じっと息をひそめているのだが、一人の人間が1つだけ足し算をした途端、何の前触れもなく世界が転換する。すべてが0に抱き留められる。
博士の愛した数式 小川洋子

これ、「eπi + 1 = 0」の式のことを言っているんだと思うんだけど、この数式の事がよく分からなくて・・・。これって一体何?
![]()

ああ、これはね、オイラーの公式のことを言ってるのよ。一般的に書けば、こういう公式なんだけど・・・。
![]()

角度φにπを代入したら、「eπi + 1 = 0」になるでしょ?

うん。

果ての果てまで循環する数って三角関数の事を言っているのよ。sinとcosって-1から1の間をずっと回り続けるでしょ?
微分しても積分してもsinとcosを行ったり来たりして、永遠に他の数にはならないの。それを「果ての果てまで循環する数」っていう国語で表現しているんだと思うわ。

決して正体を見せない虚ろな数って言うのが虚数だよね?

うん。でも虚数ってね、高校数学だと「二乗したら-1になる数」って習うかもしれないけど、三角関数と一緒に使うと一気に色々なところに応用できるようになるの。
例えば、交流電流なんかは虚数を使ってモデル化されているのよね。現実世界の三角関数をこのオイラーの公式を使って複素数表示にする。そしたら微分も積分もやりやすいでしょ?

恥ずかしがりやな性格のiって、三角関数の概念、角度の概念とはまるで恋人同士なのよ~

1を足した瞬間0になるっていうのは?

eもπもiも掴みどころのない数字でしょ?無理数と虚数。πとiがeの下で奇跡的に出会うことによって、突然秩序のある世界に引き込まれるって意味だと思うの。

なんか・・・すごいね。こういう数学の公式をこんなに綺麗な国語で表現できるなんて。

そうね。オイラーの公式って当たり前のように使っていたんだけど、こんなにも感情移入しちゃう数式だったなんてって思うと面白いわね。
オイラーの公式を証明する

この公式って、どうやって証明するの?

え? ・・・あ。

(・・・忘れた!!どうやるんだっけ!!?)

・・・ごめん。ワタシ、分からないから、ストークに聞いてみたら?

ストーク!オイラーの公式ってどうやって証明するんだっけ!!?

色々あるが、どれにする?微分方程式使ってもいいし、テイラー展開でもできるし、ロンスキアンとかド・モアブルとか・・・

一番わかりやすいヤツ!

そうだな・・・。それやったら、テイラー展開だな。
ディープルは指数関数、三角関数の微分のハナシはついていけるか?

うん。高校数学の範囲だから大丈夫。

よし、それじゃあ、テイラー展開ってのをまず最初に説明するぜ。式にするとこんな感じだ。
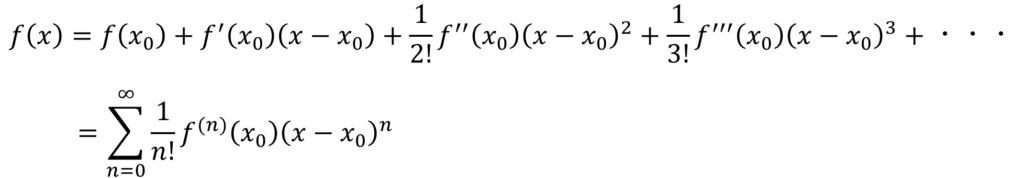

これを使えば、ある関数f(x)をn次式で表すことができるんだ。分数関数も指数、対数も三角関数も全てxのn乗の和の形にすることができるから、解析学的に非常に便利なテクニックなんだ。この式はある関数f(x)のx0周りでのn次式への近似を表している。
シママはテイラー展開、わかるよな?

うん。パンキョーの数学で出てくるヤツでしょ?受験テクニックとしても習った気がする。

まぁ、そうだな。大学1年生の解析学あたりで出てくるし、受験テクニックとしても使われる。
そんなテイラー展開なんやが、x0周りではなく、ゼロ周りで近似したものを特にマクローリン展開という。
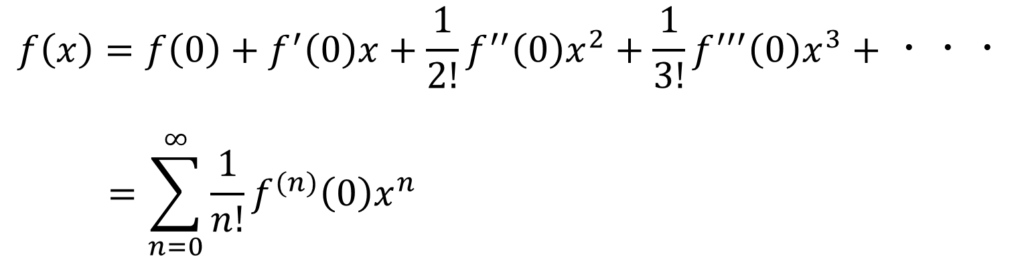

女子高生のスカートをマクローリン展開せよってな!

(・・・うあ、しょーもな~)

・・・・。

(うそ・・・、滅多に笑わないディープルが笑ってるし・・。)

それじゃあ、まずはexをマクローリン展開するぞ~(笑)!

うん!

(やだもう・・・こいつら・・。)
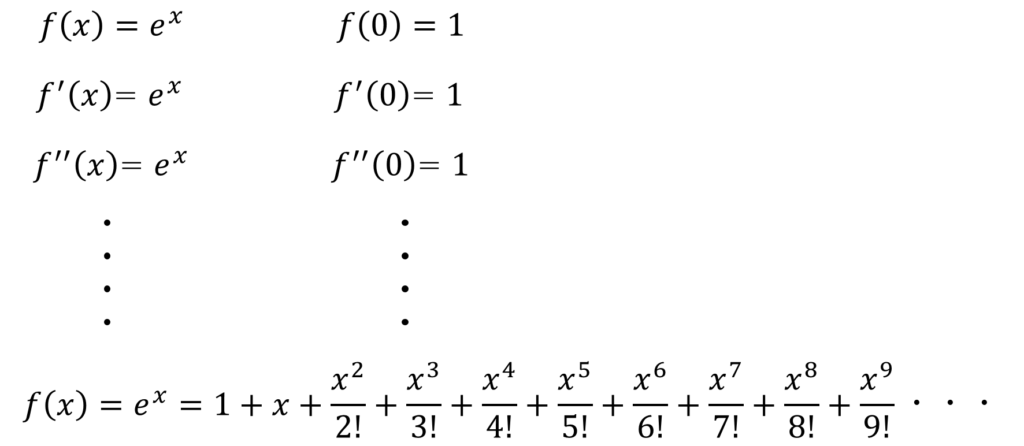

exはいくら微分しようともexのままなんで、微分係数の項は全て1だ。ここにオイラーの公式にあるiφを代入してやるけん。
その際、虚数iというものは冪の数字が増えるにしたがって、i,-1,-i,1・・・を永遠に繰り返すという性質を知っておこう。
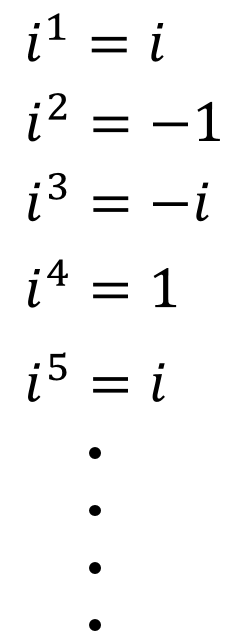
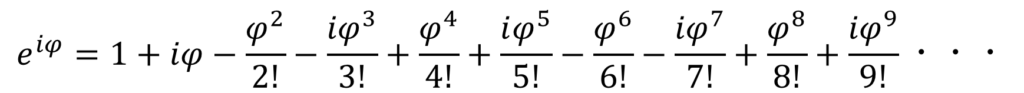

これでとりあえず、exのマクローリン展開は終わりだ。

同じようにcosとsinもマクローリン展開するぞ~(笑)!

・・・・。
cosxのマクローリン展開
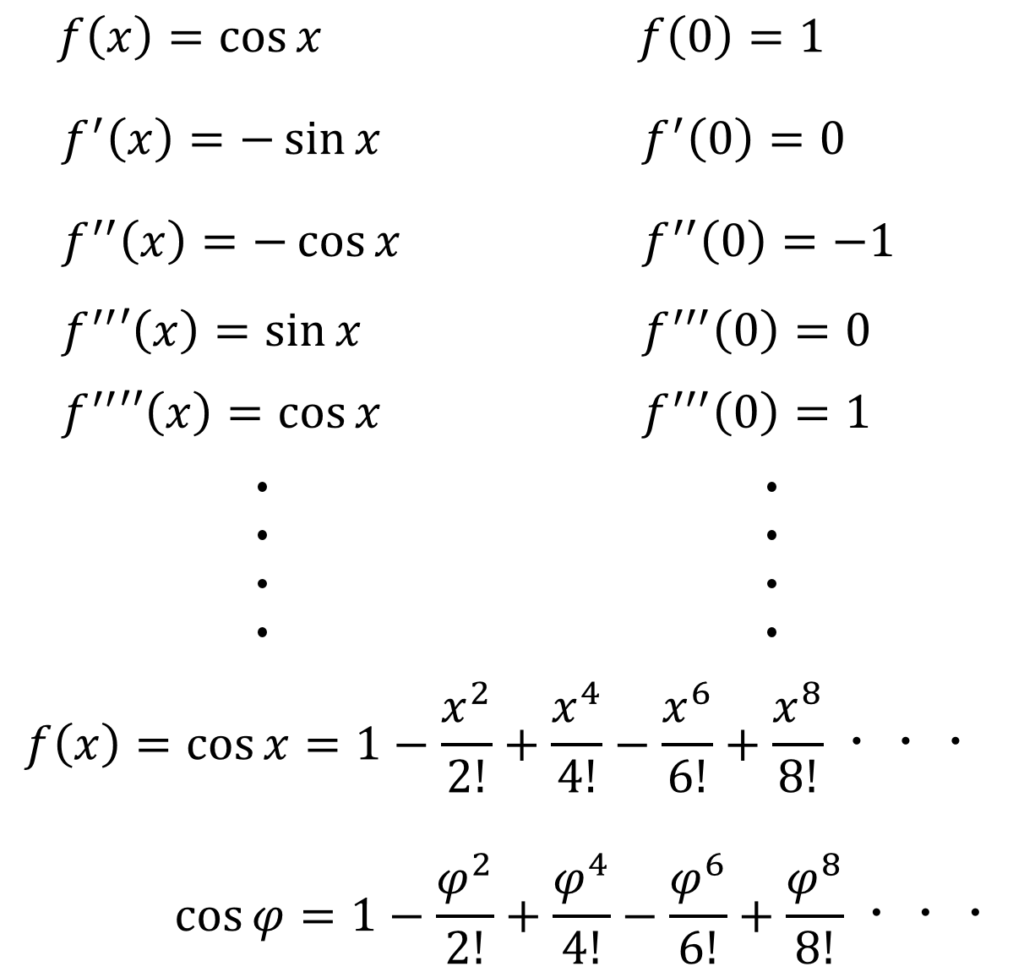
sinxのマクローリン展開
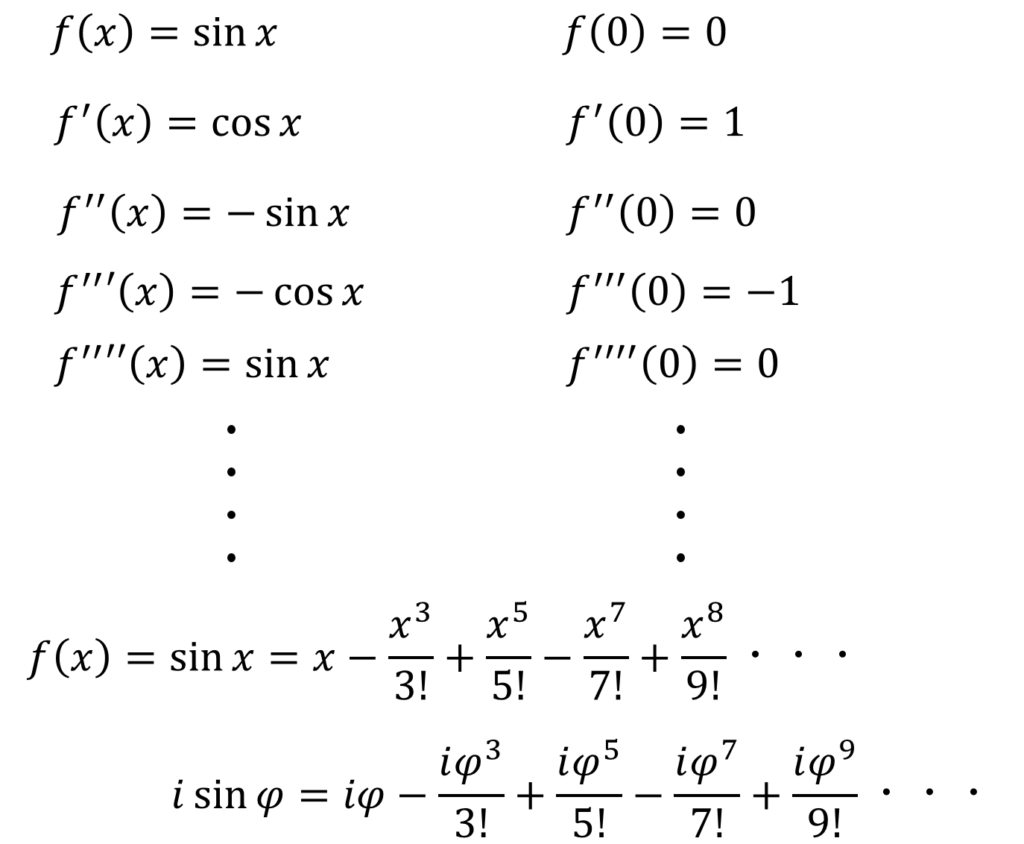

あ!これ・・・。足したらexのマクローリン展開になるね!

気づいた?cosのマクローリン展開とsinのマクローリン展開を足し合わせるとeのマクローリン展開になるんだ。
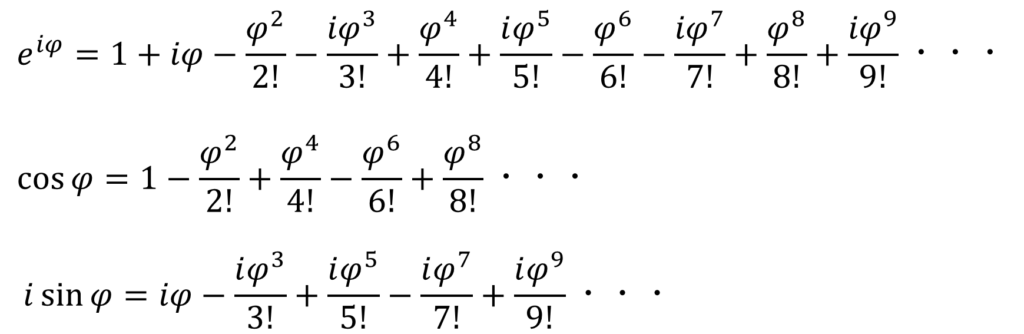

スゴイ!マクローリン展開すごいね!

すごいやろ?マクローリン展開。これでオイラーの公式の証明は終わりだ。

へぇ~ありがと!

・・・ありがとう。ストーク。
(・・・・はぁ、せっかくのロマンティックな数式が全て台無しになった気がする。)
 らい・ぶらり
らい・ぶらり


オイラー等式の数学的雰囲気は、
[絵本][もろはのつるぎ]で・・・