資料請求番号:TS11
ここには、色々なエクセルで描画することを想定して、色々なサイクロイドの式を媒介変数表示でまとめています。
サイクロイドの詳しい説明はこちら
[blogcard url=”https://shimaphoto03.com/science/cycloid/”]
他にもリマソン、バラ曲線など色々な曲線の媒介変数表示をこちらの記事にてまとめています。併せてどうぞ!
[blogcard url=”https://shimaphoto03.com/science/math-curve/”]
サイクロイド
円が直線の上を回転する時の円上の定点が描く軌跡として得られる平面曲線をサイクロイドといい、以下の式で表現できる。

イメージ
リアルタイム描画 θ = 0π~5π
内サイクロイド・ハイポサイクロイド・アステロイド
円が他の円の内周を回転する時の円上の定点が描く軌跡として得られる平面曲線を内サイクロイドまたはハイポサイクロイドといい、以下の式で表現できる。
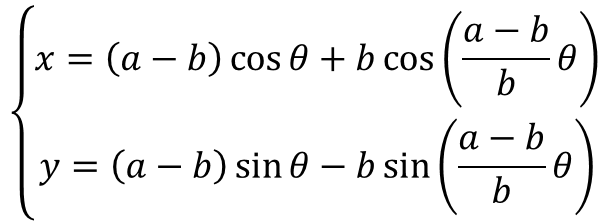
a=大円の半径、b=小円の半径
または、
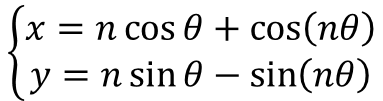
半径1の大円と半径1/(n+1)の小円
イメージ
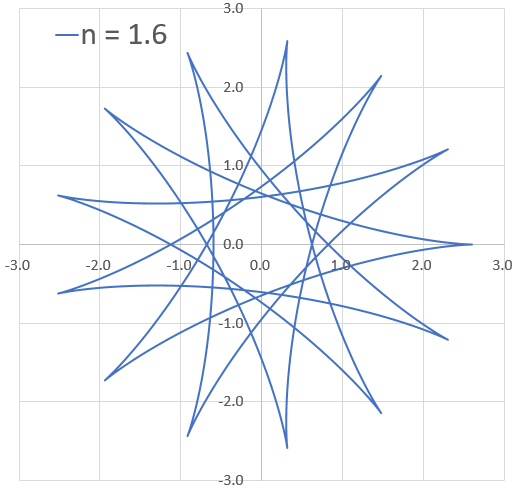
定数と曲線の形 n=2~100 1刻み
定数と曲線の形 n=1.1~5.0 0.1刻み
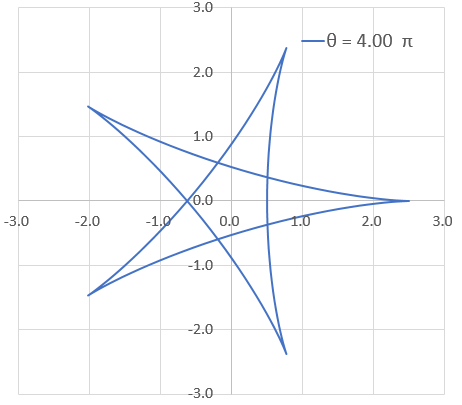
リアルタイム描画 n = 1.5, θ = 0π~4π
特にn=3のとき、アステロイドという。

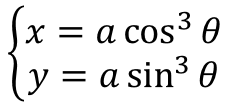
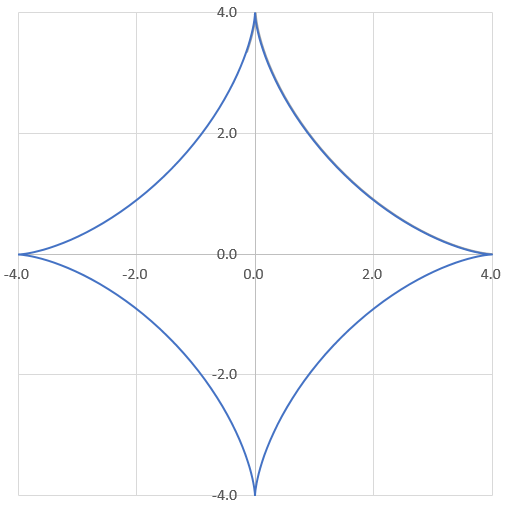
※a = 4
外サイクロイド・エピサイクロイド・カージオイド
円が他の円の外周を回転する時の円上の定点が描く軌跡として得られる平面曲線を外サイクロイドまたはエピサイクロイドといい、以下の式で表現できる。
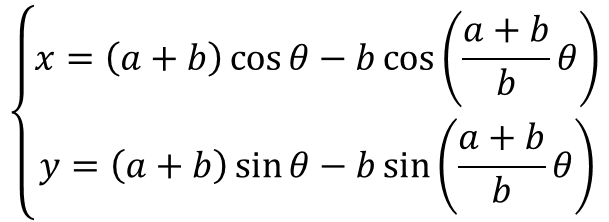
a=大円の半径、b=小円の半径
イメージ
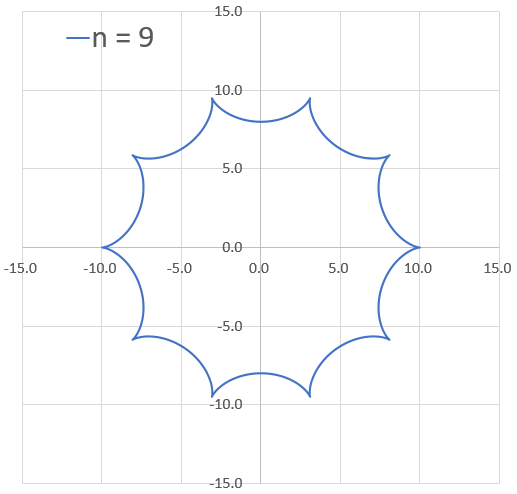
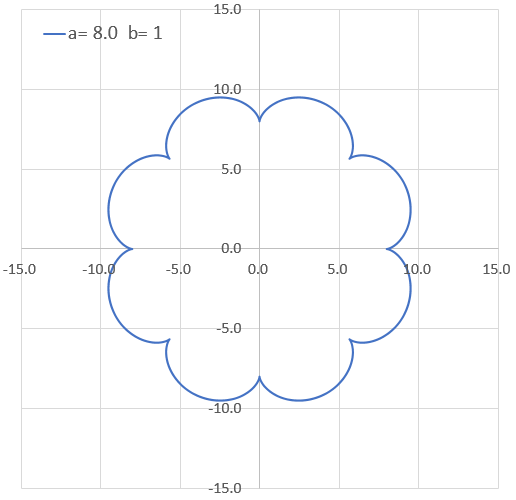
定数と曲線の形 a=2~100 1刻み
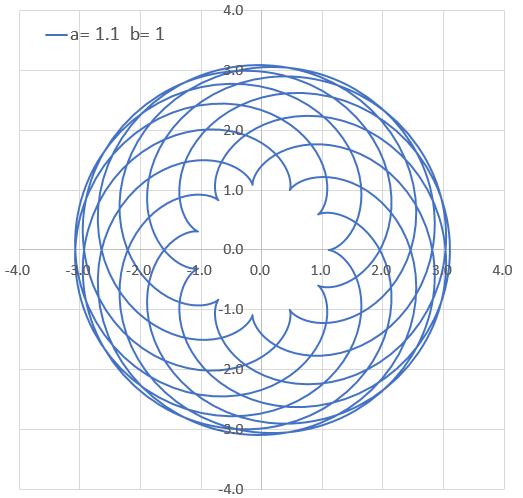
定数と曲線の形 a=1~5.0 0.1刻み
リアルタイム描画 a = 1.2, b=1, θ = 0π~10π
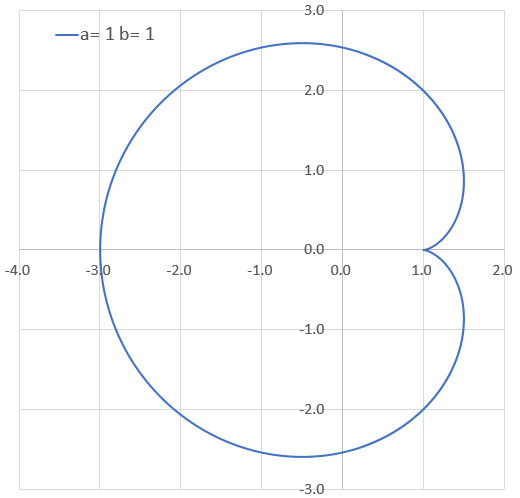
特にa=1, b=1のとき、カージオイドという。

 らい・ぶらり
らい・ぶらり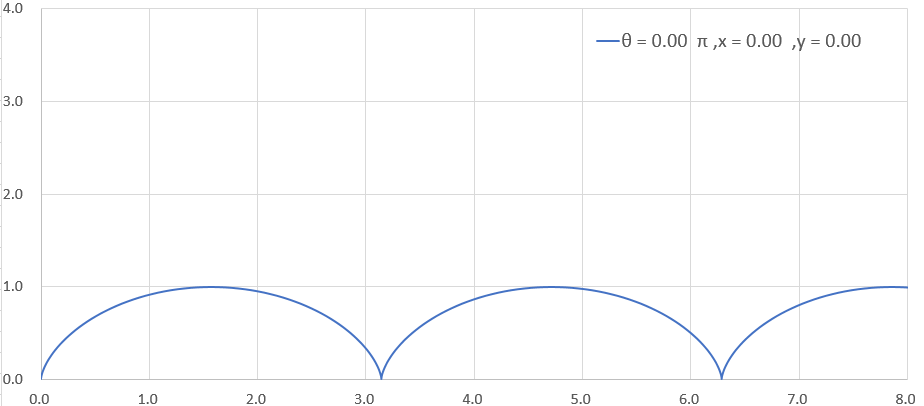
コメントを残す