資料請求番号:TS11 TS12
スポンサーリンク円周率が3.05よりも大きいことを証明する
円周率が3.05より大きいことを証明せよ
出典:東京大学 入学試験過去問題
こんなに短い数学の問題は非常に珍しいです。
そして、こんなにも易しい東京大学の入試問題も非常に珍しいです。
この問題は、2003年の入試問題のようで、2002年から始まったゆとり教育への東大からのメッセージか?と意見を述べる方も多いようです。
また、2007年放送のドラマ「受験の神様」第3話にもこの問題は登場しました。成海璃子さんが涼しい顔してサッサと解答を進め、
周りの人を唖然とさせたシーンが頭の片隅に残っている方もいるかと思います。
今回はこの円周率が3.05よりも大きいことを証明せよ。という問題をやってみたいと思います。
問題をやった後、「この問題はゆとり教育とは関係ない」という私の意見と、この問題の個人的解釈をまとめてみました。
証明
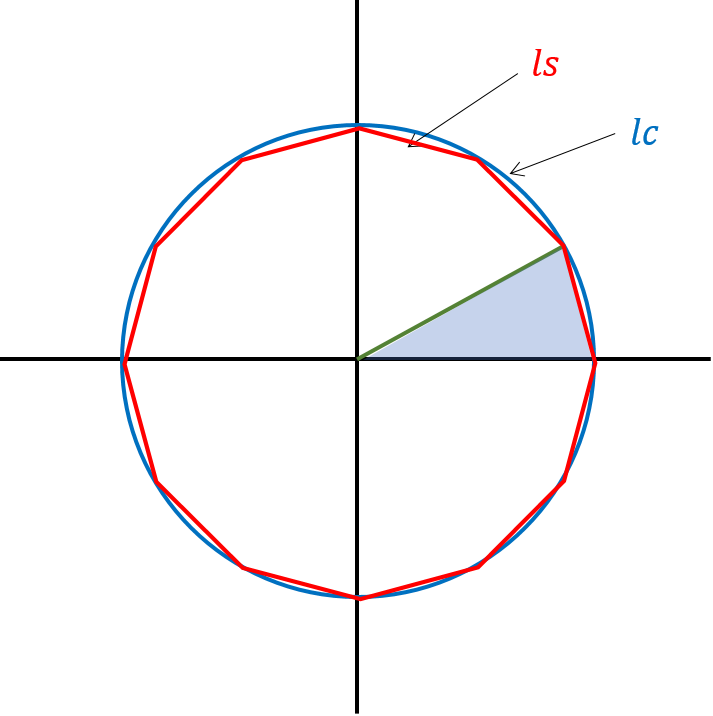
正八角形を使う場合
半径1の円を用意し、それに内接する正8角形を描きます。ドラマでは正12角形に分割しておりましたが、実は正8角形でもこの問題はできます。
円周の長さをlc、正八角形の周の長さをlsとします。
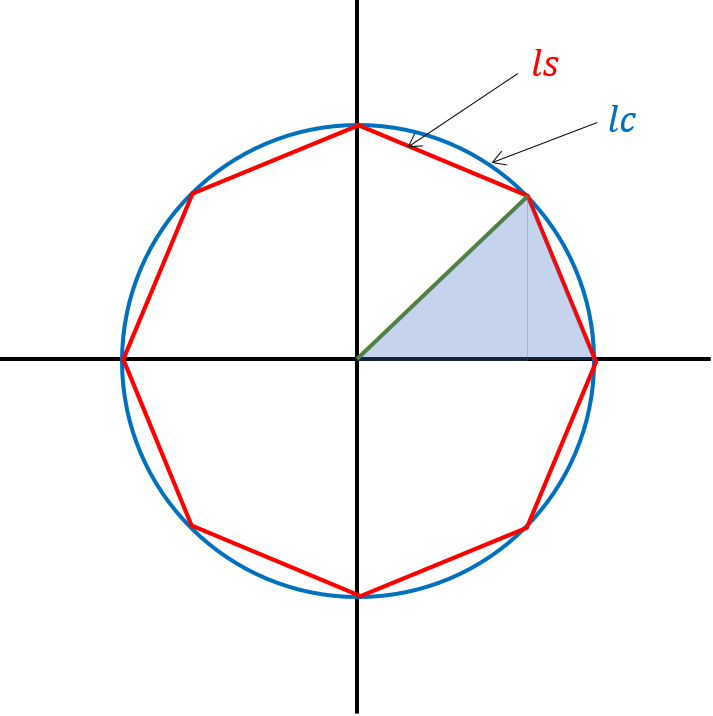
中心から正八角形の頂点に線を伸ばし、出来上がる三角形を見てみます。
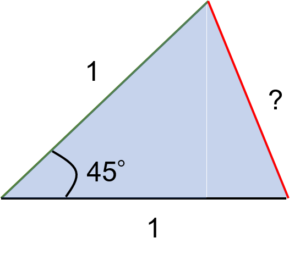
黒線、緑線の長さはそれぞれ1、それをなす角は45°です。
三角形の2辺とその間をなす角が分かれば、残りの1辺の長さは余弦定理で求まります。
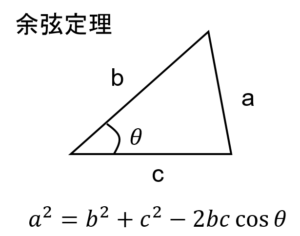
この公式を、今回の三角形に当てはめれば、赤線の長さ、すなわちlsの1/8が分かるのです。
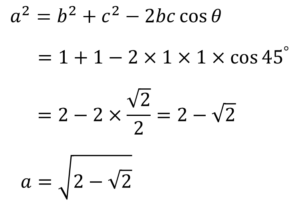
このとき、
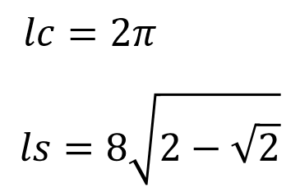
が成り立ちます。ここで、lc>lsより
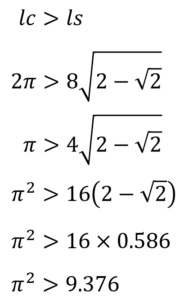
√2 = 1.414としました。途中で不等式を2乗しておりますが、右辺も左辺も0以上であるという条件を満たしていることが明らかであるため、このような式変形が可能となります。
3.05の2乗は9.30なので9.376>9.30より
円周率πが3.05より大きいことが証明されます。
正十二角形を使う場合
では、ドラマと同じように正12角形でやってみましょう。
同じように、余弦定理を使って式変形していきます。

日常的に計算を行う研究や仕事をしている方だったら、31の2乗の値が961であるということはすぐにでてきます。したがって、
正十二角形を使えば3.05どころか、3.10よりも大きいことが証明出来てしまうことに気づきます。
因みに、ドラマでは「加法定理を用いた証明に移りますが・・・・」と言っておりますが、
今回注目した三角形の頂点から底辺に垂線を降ろすと、15°、75°、90°より構成される直角三角形が出来ますので
ls = 24×sin15°となり、ここからlsを求めることができます。15は30の半分ですので、加法定理を使ってsin15°を求めることができます。
所見

この解答で配点の満点がもらえるかどうかはわからん。
もっと高校数学の範囲内で数学的に美しい方法を東大の先生は求めているのかもしれない。
シママはこの問題についてどう思う?

どう思うって・・・?時期も時期だし、
ゆとり教育で円周率を3として小学生に教えていることに対しての問題提起じゃないの?

う~ん。ネットを見てもそういう事が書かれている記事がたくさんあるが・・・。
俺は違うと思うたい。

え??

まず、円周率を3として小学生に円の面積を求めさせていることが「ゆとり」の始まりだと言っているが、別に3で計算しようが3.14で計算しようが、学習のレベルは同じやろ? 面積A = πr2を教えていることには何ら変わりはない。めんどくささが変わるだけや。簡単になったわけではないったい。
さらに、中学生に上がればπはπとして取り扱う。円周率が3で計算して育った子ども、3.14で計算して育った子ども。差がつくとは思えんたい。

ふぅ~ん・・・・。じゃあ、この問題との関係は?

たまたまやろ?それか、教授が「なんか、円周率が盛り上がってるから、それがらみの問題だそう」とでも思ったんじゃないのか?
真実は知らねぇけどな。少なくとも真実は誰も知らねぇのに、あたかもこの問題が「円周率は3と計算する」ことに対する批判であるとして、ムダに盛り上がってるのが気分悪いたい。

ゆとりゆとりうるさいもんね~。世の中のお年寄りは私たちの世代を批判したくてしょうがないからね。

まぁな。どんな世代もそうだけど、残念かな。レッテル貼りしたいのが、人間の本能のようやからな。

じゃあ、この問題、何を問うているのかしら?使った定理って余弦定理だけでしょ?加法定理でもいいけど・・・
とにかく、誰でも知ってる定理を一つだけ使って完結しちゃう問題なんて東大らしくないら?

ああ。俺も東大らしくないと思っている。

ただし、これは数学的に非常に面白い問題やけん。
これ、古代バビロニアにおけるπの求め方やアルキメデスによるπの求め方と同じことをさせとる。
円をたくさんの三角形に分割させて近似する。その三角形の数が無限大になった時、円に収束する。
俺はこの問題から「色々な受験数学のテクニックやるのもいいけどさ、初心に帰って数学を楽しもうよ」
というメッセージを感じるったい。俺はこの問題をそう解釈するたいね。

そっか・・・。東大受験生は大量の数学の問題を解いて、テクニックを身に着けているもんね・・・。
例えば、ルートのかかった4-x2を積分するなら、xを2sinθって置くとか・・・。

ああ。東大受験生でもしこの問題に手も足もでなかったとしたら、おそらくソイツはテクニックロボットやろうな。
テクニックに執着しすぎてて、「πはそもそもどこからやってきたのか?」とか本質を考える能力がないんだ。
もしかしたら、この問題はそういう受験生を切り捨てるためにあるのかもしれないったいね。

πどころか、複雑な図形を分割して小さな要素の集合体として考えるという考え方は数学、詳しく言えば微分積分の基本だら?

そうなんだ。オマエもそう思うやろ??
テクニックも大事だが、そもそもπってなんだ?微分積分ってなんだ?級数ってなんのためにあるんだ?
昔の人はどうして指数対数三角関数っていう概念を取り入れたんだ?そしてなぜ、その考え方が今になっても理論として成立しているんだ?
って興味を持ちながら勉強したほうが数学は伸びると思うとる。

そういう意味では、この問題は「おい、学問を楽しんどるか?」と、問うて「はい」と答えるヤツに合格させたい。
少なくとも、おいはそういうヤツと勉強したいたい。もしかしたら、これを出した教授も同じなんじゃないやろか?

なるほど・・・面白いわね。
(たまたまって言ってたくせに・・・。コイツ、すっごい論理的だけど、感情移入すると論理的思考が少し鈍るのよね・・・。)

まぁ、この東大の問題から何を感じ取るかは人それぞれなんやが、少なくとも俺はそう思うたい。
 らい・ぶらり
らい・ぶらり


コメントを残す