資料請求番号：TS31
東海道線に乗っていたら、「富士山の体積をはかるアイデア大募集！」という広告を見つけました。
詳しく調べてみると、静岡県建設コンサルタンツ協会が「はかる楽しさ」を知ってもらおうとアイデアを募集しているとのこと。
CON!CON! 富士山の体積をはかる「アイデア」を大募集！
コンコン！キツネのキャラクターが可愛らしいですね。コンストラクト（建設）・コンサルタントから来ているのでしょうか？
本記事では、2種類のアイデアをまとめてみたいと思います。
この方法は富士川河川敷で撮った写真を使って富士山の峰の形状を関数に落とし込み、富士山は軸対称系であると仮定して、峰の関数を標高について積分することによって体積を求める方法です。
ねぇねぇ！ストーク！シママ！
なんだよ。
なに？
あのね、こないな、電車にこんな広告があったけん、ストークやシママならこういうの得意そうかな～思て。
出典：CON!CON! 富士山の体積をはかる「アイデア」を大募集！
富士山の体積？
ああ、そういえばこないな、数検1級の問題で富士山の表面は調和関数になると仮定して、ラプラス方程式解いて、富士山の峰の形を求めたことがあったよなぁ、シママ。
うん。あったあった。峰の形は対数関数に近似できるってヤツでしょう？
せやせや。これ応用すれば体積は求められるたいね。
？？？
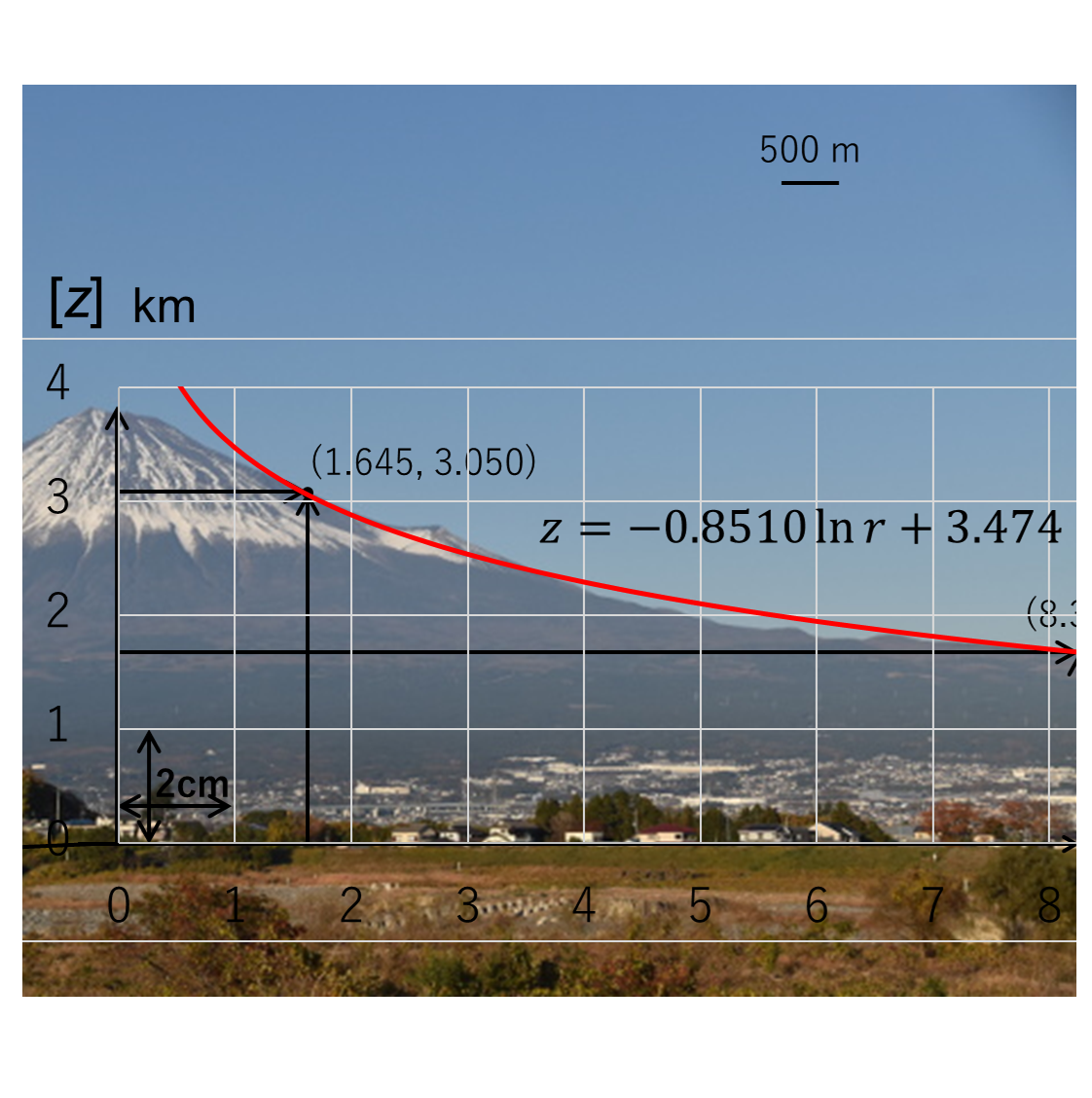
ファビーな、zが標高で、rが火口中心からの距離たい。そしたら、火口中心からr[km]における標高z[km]はこの式に従うってことたい。以前、この関数を求めることをシママとやってたんよ。
lnってなに？
ああ、それはあれよ。log。lnrってのはlogerってこと。eはネイピアの数で2.718くらいの定数。
logはホラ、高校数学Ⅱで出てくるでしょ？
あのな、微分方程式解きよったら、e底のlogがクサるほど出てくるけん、めんどいからnatural logをもじってlnって表現しとるたい。
ふぅ～ん・・・。
さっきの式のから富士山の体積を求める考え方としてはな、
富士山を円柱の集合体って考えるたい。半径ri、高さzの円柱な。
これをい～っぱい積み重ねたら、富士山みたいな形になるら？
たしかに・・・・。
つまり、こうやな。円柱をぐーっさり集めて、ぐーっさり足すんよ。
ぐっさり？
ああ、熊本弁で「たくさん」っていう意味たい。
それで、円柱の高さzを細か～してdzにして、足し上げる。これが積分たいね。
問題は積分の範囲よね・・・。
せやなぁ・・・。上限は3.776として、下限をどうするかやな。一応、どの高さから測るかは自由ということやから、とりあえず、1合目の標高から測ってはどんな？
そうね！1合目の高さは1516mらしいわよ。
出典：富士登山マニュアル
ほんなら、こうやな。
えっと・・・。rが半径で、半径てのは、火口中心から山の表面までの距離で・・・。
うんうん。
半径rの円の面積πr2に微小な高さdzをかけたら、うすべったい円柱の体積になって
せやせや。dV = πr2dzやな
それを、高さ1.516kmでのうすべったい円柱の体積と1.516+dz[km]のうすべったい円柱の体積と・・・ってぐ～っさりやって、それを3.776kmまで続ける計算がこれってこと？
そう！その通り！
考え方が分かったら、後は計算たい。
まずは、r=f(z)の形にしないとね。
せやな。そしたらあとは、これに当てはめて・・・
こうしたら・・・答えは132.5km3たいね。
お～っ！！
2乗の計算がexpの冪の2倍になるから凄く都合がいいわね。
せやな。あと、関数がexpだから積分がラクやったな。
ファビー、こんときの裾野の面積はな、高さ1.516kmにおける円の面積たいね。計算してみな。
えっと・・・・。rがこの式で・・・
z=1.516を代入しよったら、rは9.982kmになって・・・
半径×半径×3.14やから、面積は・・・313.1km2
せやな！
やった！
あ～・・。さっきはあれね。高さ1.516km以上を富士山と定義した体積だったわね。
今度は裾野の半径なんとかkm以下を富士山とするっていう定義による計算もできるわね。
せや。それやと、静岡県建設コンサルタンツ協会が求めた方法に近いやり方で体積が求められるたい。
火口中心から北東へ進んで富士急行線の富士山駅近くの国道138号線までの距離を半径としよか。
そしたら、その距離は14.48kmになるたい。
ホントはな、θ=0~2πの範囲で0.2π刻みで火口中心からの距離求めて平均とったり、1km四方の正方形描いて、これを敷き詰めて面積求めたりせなあかんと思うけど、
これは仕事じゃないけん、めんどいからやらん。そういう意味でかなり粗い近似だけん、半径15㎞でええやろ。
まぁ、それ言いだしたら、富士山を軸対称の立体とするという仮定もアカン思うたいね。火口から見て東西南北すべて峰の形は違って、-0.8510と3.474の定数は変わるやろうな。
こういう問題、精度求めようとしたらキリないよなぁ～。
あ～わかるなぁ～その気持ち・・。
複雑な問題だからね。どこまで仮定をして何に近似したって言うのをちゃんと明示した上で、妥協しないといけないのよね。
妥協いうと悪くきこえるけど、ホンマの富士山の体積求めたかったら、山切りくずさんといかんたい。
そないなこと、一生できんからな。
ま、とりあえず今回は火口中心から半径15㎞を裾野と定義するのね。
せやな。そしたら、この式で、半径15㎞地点における富士山の高さを求めるたいね。
高さは1.169kmか～。標高1169mね。
そしたら今度はこれを計算することになるんやろ？
そうそう！
そしたら・・・お、ちょうど300km3や。
さっきの答えと倍くらい変わったんね。
山はな、標高が低ければ低いほど体積デカなるからな。
標高ナントカkmとか、裾野の半径ナントカkmで随分答えが変わっちまう。
そういう意味で、基準てのは明確に示さなアカンよな。
そっか～。単に富士山の体積はいくついくつです～いうよりも、
標高何m以上を富士山としたら体積はいくつです～って言った方が信じられるけんね。
せやな。ちなみに標高0mから富士山としたら体積は4697km3になるたい。
でもそれ、裾野の半径は・・・59.3㎞やろ？静岡市越えて島田まで富士山とか意味わからん。
まぁ、そういう実際の現象？っーか、この場合は地形か。地形と照らし合わせてイカれた答え出しとらんか考えるのも大事たいな。
富士川河川敷で撮った写真を使って富士山の峰の形状を関数に落とし込み、富士山は軸対称系であると仮定して、峰の関数を高さについて積分することによって体積を求める方法で富士山の体積を求めたところ、
1合目の標高1516m以上を富士山とする場合、その体積は132.5km3であり、
富士山の裾野の半径15㎞とする場合、その体積は300.4km3でした。
この方法で体積を求める場合、標高z0［km］以上が富士山であるとしたら、体積は以下の通りになります。
また、裾野半径r0［km］の標高z0［km］となり、それ以上が富士山であるとしたら、体積は以下の様になります。
いや～数学のチカラって凄いんね！富士山の体積までわかっちゃうなんて～
まぁ、メチャクチャ概算・・・ええかげんやけどな。
これで応募してみたらどない？
ハハッ（笑）応募はせんよ。
なんで？
やってさぁ～この動画みてみ？
CON!CON! 富士山の体積をはかる「アイデア」を大募集！
それからこのページには「審査基準は、答えの正確さではなく、はかることの楽しさを教えてくれること」って書いてあるたいね？
こんな微分積分使った回答が客観的に観ておもろいわけないやろ？
確かに・・・。
こう・・・なんつーかな？俺らの回答はエンターテイメント性がなか。
エンターテイメント性？
例えばホラ、テレビのクイズ番組でさ、IQクイズみたいなモノは出されるけど、微分積分・微分方程式使って解くような問題は出されないら？
それって、客観的に観て高等数学が面白いって思われてない証拠なのよ。
せや。今回の挑戦状の目的は測量や設計の仕事の面白さを知ってもらうのが目的だけん、そこに、ログ・イクスポネンシャル・インテグラルだ～って。
エンタの神様で数学の授業するのと同じくらい滑稽たい。
エンタの神様なつかし～（笑）
エンターテイメント性求めるんやったらな～。どんな方法がええかな～・・・・。
なんかこう・・・ある標高における富士山の断面の面積を面白おかしく測る方法がええけんね～・・・。
富士山の断面の面積を面白おかしく測る・・・・。
せやせや、それこそIQクイズみたいな考え方がええたいね～。
ぶっとんだ方法がええなら、こんなんはどう？
巨大なビーズを作るけん。
巨大なビーズ？
ゆーめーじゃないあれもこれも～♪
そのB’zちゃうねん。シママもちーさいころ遊んだことあるやろ？ビーズを使ってキラキラしたかわいいものを作ったやろ？
あ～・・・うん。
（ワタシ、小さい頃は男の子と混じって秘密基地づくりとかザリガニ採りとかしてたからあまりしてないのよね・・・・。）
んでな、普通ビーズって糸通してつなげるけど、この問題ではバネ通してつなげる・・・というか、球と球の間にバネを溶接したりするけん。
うん。
そーやって、円をつくるけん。こんな感じ。
これを飛行機から落としまくるんよ～。
大災害やな～（笑）
我ながらぶっ飛んでる思うけんね～。
そしたら、この円がバネを伸ばしながら、ドッシンゴロゴロなって標高の低いところではバネが伸びて、高いとこではそんなに伸びない。
球の数をキチンと決めて落とせば、ある標高において、球と球の距離から円周が分かるけんね。
あ～なるほど～そうやってある標高における高さにおける富士山の円周が分かって面積がわかるから、それを足し上げれば体積になるのね～。
そのバネのついたヤツは回収できねぇ、落として山小屋はメチャクチャにする、そないなデカいもん飛行機に載せられへん、バネが一様に伸びるとは限らんっていうロクでもないアイデアやけど、考えるだけなら楽しいたいね。
せやろ～（笑）
今回は、富士山の体積をはかるアイデア大募集！の広告を見て、富士山の体積の出し方を2種類考えてみました。
CON!CON! 富士山の体積をはかる「アイデア」を大募集！
一つ目は写真を使って峰の形を以下のように関数に落とし込み、富士山は軸対称であると仮定して、標高zに関する積分を行って体積を求める方法
標高z0［km］以上が富士山であるとしたら、体積は以下の通りになります。
また、裾野半径r0［km］の標高はz0［km］となり、それ以上が富士山であるとしたら、体積は以下の様になります。
二つ目は、球の数をn個と決めて球とバネを円形に繋ぎ
これを飛行機から落としたあと、球と球の長さ×nで円周を求め、ある標高における富士山の断面積を計算、その断面積を足し上げて体積を求める方法
二つ目は半分オマケみたいなものです。
この問題な～基準が自由ゆうなら、山頂だけ、しかも剣が峰にある石ころ一つだけ富士山だって言い張れば、
剣が峰に行って石ころ拾ってくればええたい。それをメスシリンダーに入れれば、体積はかれるたいね～。
なんやねんそれ（笑）それやったら、はかる楽しさじゃなくて登る楽しさになっちゃうけんね～（笑）
あとな～。富士山の体積を1[Fuji]とする。っていう体積の単位の定義を作って、
富士山の体積は1[Fuji]であるって言い張るとかな。
もっとアホらしいわぁ～。そういうのヘリクツっていうけんね。
でもな～単位の歴史って、意外にそういうアホらしくて屁みたいな理屈が多いたいね。例えば、人の足の長さを1フィートにするとかな。
1日一人が食べる小麦の質量を1ポンドにするとかね。
せやせや。一昔前の教科書はlbとかftとか多かったいね。
キログラム重[kgf]とかウザいよね～。未だに現場では1[kgf/cm2]を圧力1キロって言うしね。
まぁ、1キロはな～1気圧、工学気圧だけん、わかりやすいから残り続けとるたいね。きっと。
そんなふうに、最近まで単位の取り扱いって人々が好き好きにしていたんやけど、1950年代やったかな？SI単位を使いましょういうことになって、そこからボチボチ教科書がSI単位に統一されて来とるんよな。
そういう単位があるんなら1[Fuji]って単位もあってもええかもな（笑）
View Comments
職場で琵琶湖に富士山が何個入るかと言う
バカな質問をして笑われた、14倍か。